|
|
|
A polynomial given by
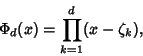 |
(1) |
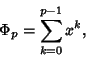 |
(2) |
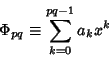 |
(3) |
| (4) |
| (5) |
The Logarithm of the cyclotomic polynomial
| (6) |
The first few cyclotomic Polynomials are
The Polynomial ![]() can be factored as
can be factored as
| (7) |
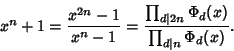 |
(8) |
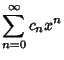 |
(9) |
| (10) |
See also Aurifeuillean Factorization, Möbius Inversion Formula
References
Beiter, M. ``The Midterm Coefficient of the Cyclotomic Polynomial
Beiter, M. ``Magnitude of the Coefficients of the Cyclotomic Polynomial
Bloom, D. M. ``On the Coefficients of the Cyclotomic Polynomials.'' Amer. Math. Monthly 75, 372-377, 1968.
Carlitz, L. ``The Number of Terms in the Cyclotomic Polynomial
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, 1996.
de Bruijn, N. G. ``On the Factorization of Cyclic Groups.'' Indag. Math. 15, 370-377, 1953.
Lam, T. Y. and Leung, K. H. ``On the Cyclotomic Polynomial
Lehmer, E. ``On the Magnitude of Coefficients of the Cyclotomic Polynomials.'' Bull. Amer. Math. Soc. 42, 389-392, 1936.
McClellan, J. H. and Rader, C. Number Theory in Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1979.
Migotti, A. ``Zur Theorie der Kreisteilungsgleichung.''
Sitzber. Math.-Naturwiss. Classe der Kaiser. Akad. der Wiss., Wien 87, 7-14, 1883.
Schroeder, M. R.
Number Theory in Science and Communication, with Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity, 3rd ed.
New York: Springer-Verlag, p. 245, 1997.
Sloane, N. J. A. Sequence
A013594
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 8 and 224-225, 1991.
![]() .'' Amer. Math. Monthly 71, 769-770, 1964.
.'' Amer. Math. Monthly 71, 769-770, 1964.
![]() .'' Amer. Math. Monthly 75, 370-372, 1968.
.'' Amer. Math. Monthly 75, 370-372, 1968.
![]() .'' Amer. Math. Monthly 73, 979-981, 1966.
.'' Amer. Math. Monthly 73, 979-981, 1966.
![]() .'' Amer. Math. Monthly 103, 562-564, 1996.
.'' Amer. Math. Monthly 103, 562-564, 1996.
|
|
|
© 1996-9 Eric W. Weisstein