|
|
|
The finite difference is the discrete analog of the Derivative. The finite Forward Difference of a function
![]() is defined as
is defined as
| (1) |
| (2) |
| (3) |
However, when ![]() is viewed as a discretization of the continuous function
is viewed as a discretization of the continuous function ![]() , then the finite difference is
sometimes written
, then the finite difference is
sometimes written
| (4) |
| (5) |
An ![]() th Power has a constant
th Power has a constant ![]() th finite difference. For example, take
th finite difference. For example, take ![]() and make a Difference Table,
and make a Difference Table,
 |
(6) |
Finite difference formulas can be very useful for extrapolating a finite amount of data in an attempt to find the general
term. Specifically, if a function ![]() is known at only a few discrete values
is known at only a few discrete values ![]() , 1, 2, ... and it is desired to
determine the analytical form of
, 1, 2, ... and it is desired to
determine the analytical form of ![]() , the following procedure can be used if
, the following procedure can be used if ![]() is assumed to be a
Polynomial function. Denote the
is assumed to be a
Polynomial function. Denote the ![]() th value in the Sequence of interest by
th value in the Sequence of interest by ![]() . Then define
. Then define ![]() as the
Forward Difference
as the
Forward Difference
![]() ,
, ![]() as the second Forward Difference
as the second Forward Difference
![]() , etc., constructing a table as follows
, etc., constructing a table as follows
|
|
|
|
|
|
|
|
|
|
|
(7) |
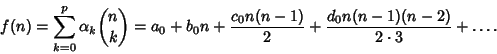 |
(8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (9) |
Beyer (1987) gives formulas for the derivatives
| (10) |
| (11) |
Finite differences lead to Difference Equations, finite analogs of Differential Equations. In fact, Umbral Calculus displays many elegant analogs of well-known identities for continuous functions. Common finite difference schemes for Partial Differential Equations include the so-called Crank-Nicholson, Du Fort-Frankel, and Laasonen methods.
See also Backward Difference, Bessel's Finite Difference Formula, Difference Equation, Difference Table, Everett's Formula, Forward Difference, Gauss's Backward Formula, Gauss's Forward Formula, Interpolation, Jackson's Difference Fan, Newton's Backward Difference Formula, Newton-Cotes Formulas, Newton's Divided Difference Interpolation Formula, Newton's Forward Difference Formula, Quotient-Difference Table, Steffenson's Formula, Stirling's Finite Difference Formula, Umbral Calculus
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Differences.'' §25.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 877-878, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 429-515, 1987.
Boole, G. and Moulton, J. F. A Treatise on the Calculus of Finite Differences, 2nd rev. ed. New York: Dover, 1960.
Conway, J. H. and Guy, R. K. ``Newton's Useful Little Formula.'' In The Book of Numbers. New York:
Springer-Verlag, pp. 81-83, 1996.
Iyanaga, S. and Kawada, Y. (Eds.). ``Interpolation.'' Appendix A, Table 21 in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1482-1483, 1980.
Jordan, K. Calculus of Finite Differences, 2nd ed. New York: Chelsea, 1950.
Levy, H. and Lessman, F. Finite Difference Equations.
New York: Dover, 1992.
Milne-Thomson, L. M. The Calculus of Finite Differences. London: Macmillan, 1951.
Richardson, C. H. An Introduction to the Calculus of Finite Differences. New York: Van Nostrand, 1954.
Spiegel, M. Calculus of Finite Differences and Differential Equations. New York: McGraw-Hill, 1971.
![]() Finite Difference Equations
Finite Difference Equations
|
|
|
© 1996-9 Eric W. Weisstein