Chebyshev Quadrature

A Gaussian Quadrature-like Formula for numerical estimation of integrals. It uses Weighting Function $W(x)=1$ in the interval $[-1,1]$ and forces all the weights to be equal. The general Formula is

$$\int_{-1}^1 f(x)\,dx={2\over n}\sum_{i=1}^n f(x_i).$$

The Abscissas are found by taking terms up to $y^n$ in the Maclaurin Series of

$$s_n(y)=\mathop{\rm exp}\nolimits \left\{{\textstyle{1\over 2... ...}\right)+\ln(1+y)\left({1+{1\over y}}\right)}\right]}\right\},$$

and then defining

$$G_n(x)\equiv x^n s_n\left({1\over x}\right).$$

The Roots of $G_n(x)$ then give the Abscissas. The first few values are

$$\begin{eqnarray*} G_0(x)&=&1\\ G_1(x)&=&x\\ G_2(x)&=&{\textstyle{1\over 3}}... ...extstyle{1\over 22400}}(22400x^9-33600x^7+15120x^5-2280x^3+53x). \end{eqnarray*}$$

Because the Roots are all Real for $n\leq 7$ and $n=9$ only (Hildebrand 1956), these are the only permissible orders for Chebyshev quadrature. The error term is

$$E_n=\cases{ c_n{f^{(n+1)}(\xi)\over(n+1)!} & $n$\ odd\cr c_n{f^{(n+2)}(\xi)\over(n+2)!} & $n$\ even,\cr}$$

where

$$c_n=\cases{ \int_{-1}^1 xG_n(x)\,dx & $n$\ odd\cr \int_{-1}^1 x^2G_n(x)\,dx & $n$\ even.\cr}$$

The first few values of $c_n$ are 2/3, 8/45, 1/15, 32/945, 13/756, and 16/1575 (Hildebrand 1956). Beyer (1987) gives abscissas up to $n=7$ and Hildebrand (1956) up to $n=9$.

$n$	$x_i$
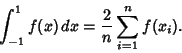
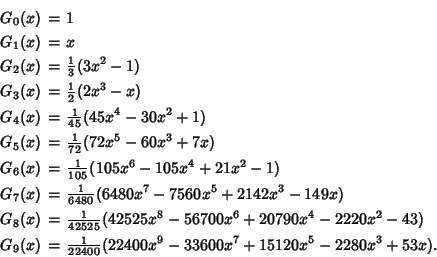
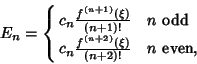
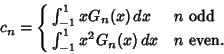
2	± 0.57735
3	0
	± 0.707107
4	± 0.187592
	± 0.794654
5	0
	± 0.374541
	± 0.832497
6	± 0.266635
	± 0.422519
	± 0.866247
7	0
	± 0.323912
	± 0.529657
	± 0.883862
9	0
	± 0.167906
	± 0.528762
	± 0.601019
	± 0.911589

The Abscissas and weights can be computed analytically for small $n$.

$n$	$x_i$
2	$\pm{\textstyle{1\over 3}}\sqrt{3}$
3	0
	$\pm{\textstyle{1\over 2}}\sqrt{2}$
4	$\pm\sqrt{\sqrt{5}-2\over 3\sqrt{5}}$
	$\pm\sqrt{\sqrt{5}+2\over 3\sqrt{5}}$
5	0
	$\pm{1\over 2}\sqrt{5-\sqrt{11}\over 3}$
	$\pm{1\over 2}\sqrt{5+\sqrt{11}\over 3}$

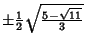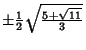See also Chebyshev Quadrature, Lobatto Quadrature

References

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 466, 1987.

Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 345-351, 1956.