Also called Chebyshev Quadrature. A Gaussian Quadrature over the interval ![$[-1,1]$](c1_1269.gif) with Weighting Function
with Weighting Function
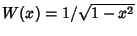 . The Abscissas for quadrature order
. The Abscissas for quadrature order 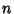 are given by the roots of the
Chebyshev Polynomial of the First Kind
are given by the roots of the
Chebyshev Polynomial of the First Kind 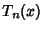 , which occur
symmetrically about 0. The Weights are
, which occur
symmetrically about 0. The Weights are
 |
(1) |
where 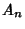 is the Coefficient of
is the Coefficient of  in
in 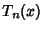 . For Hermite Polynomials,
. For Hermite Polynomials,
 |
(2) |
so
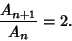 |
(3) |
Additionally,
 |
(4) |
so
 |
(5) |
Since
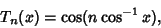 |
(6) |
the Abscissas are given explicitly by
![\begin{displaymath}
x_i=\cos\left[{(2i-1)\pi\over 2n}\right].
\end{displaymath}](c1_1324.gif) |
(7) |
Since
where
 |
(10) |
all the Weights are
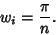 |
(11) |
The explicit Formula is then
![\begin{displaymath}
\int_{-1}^1 {f(x)\,dx\over\sqrt{1-x^2}}={\pi\over n}\sum_{k=...
...2n}\pi}\right)}\right]+ {2\pi\over 2^{2n}(2n)!} f^{(2n)}(\xi).
\end{displaymath}](c1_1331.gif) |
(12) |
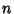 |
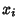 |
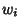 |
| 2 |
± 0.707107 |
1.5708 |
| 3 |
0 |
1.0472 |
| |
± 0.866025 |
1.0472 |
| 4 |
± 0.382683 |
0.785398 |
| |
± 0.92388 |
0.785398 |
| 5 |
0 |
0.628319 |
| |
± 0.587785 |
0.628319 |
| |
± 0.951057 |
0.628319 |
References
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 330-331, 1956.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() with Weighting Function
with Weighting Function
![]() . The Abscissas for quadrature order
. The Abscissas for quadrature order ![]() are given by the roots of the
Chebyshev Polynomial of the First Kind
are given by the roots of the
Chebyshev Polynomial of the First Kind ![]() , which occur
symmetrically about 0. The Weights are
, which occur
symmetrically about 0. The Weights are
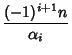
![\begin{displaymath}
\int_{-1}^1 {f(x)\,dx\over\sqrt{1-x^2}}={\pi\over n}\sum_{k=...
...2n}\pi}\right)}\right]+ {2\pi\over 2^{2n}(2n)!} f^{(2n)}(\xi).
\end{displaymath}](c1_1331.gif)