|
|
|
The word quadrature has (at least) three incompatible meanings. Integration by quadrature either means solving an Integral analytically (i.e., symbolically in terms of known functions), or solving of an integral numerically (e.g., Gaussian Quadrature, Quadrature Formulas). The word quadrature is also used to mean Squaring: the construction of a square using only Compass and Straightedge which has the same Area as a given geometric figure. If quadrature is possible for a Plane figure, it is said to be Quadrable.
For a function tabulated at given values ![]() (so the Abscissas cannot be chosen at will), write the
function
(so the Abscissas cannot be chosen at will), write the
function ![]() as a sum of Orthonormal Functions
as a sum of Orthonormal Functions ![]() satisfying
satisfying
| (1) |
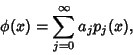 |
(2) |
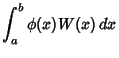 |
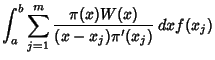 |
||
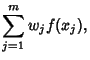 |
(3) |
![\begin{displaymath}
\int_a^b \sum_{j=0}^\infty a_jp_j(x) W(x)\,dx
= \sum_{i=1}^n w_i\left[{\,\sum_{j=0}^\infty a_j p_j(x_i)}\right].
\end{displaymath}](q_578.gif) |
(4) |
 |
(5) |
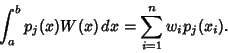 |
(6) |
| (7) |
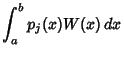 |
(8) | ||
 |
(9) |
![\begin{displaymath}
\left[{\matrix{
p_0(x_1)&\cdots&p_0(x_n)\cr
p_1(x_1)&\cdot...
...}}\right]
= \left[{\matrix{1\cr 0\cr \vdots\cr 0\cr}}\right],
\end{displaymath}](q_586.gif) |
(10) |
See also Calculus, Chebyshev-Gauss Quadrature, Chebyshev Quadrature, Derivative, Fundamental Theorem of Gaussian Quadrature, Gauss-Jacobi Mechanical Quadrature, Gaussian Quadrature, Hermite-Gauss Quadrature, Hermite Quadrature, Jacobi-Gauss Quadrature, Jacobi Quadrature, Laguerre-Gauss Quadrature, Laguerre Quadrature, Legendre-Gauss Quadrature, Legendre Quadrature, Lobatto Quadrature, Mechanical Quadrature, Mehler Quadrature, Newton-Cotes Formulas, Numerical Integration, Radau Quadrature, Recursive Monotone Stable Quadrature
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Integration.'' §25.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 885-897, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, pp. 365-366, 1992.
|
|
|
© 1996-9 Eric W. Weisstein