|
|
|
An array is a ``list of lists'' with the length of each level of list the same. The size (sometimes called the ``shape'')
of a ![]() -dimensional array is then indicated as
-dimensional array is then indicated as
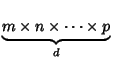 . The most common
type of array encountered is the 2-D
. The most common
type of array encountered is the 2-D ![]() rectangular array having
rectangular array having ![]() columns and
columns and ![]() rows. If
rows. If ![]() , a square array
results. Sometimes, the order of the elements in an array is significant (as in a Matrix), whereas at other times,
arrays which are equivalent modulo reflections (and rotations, in the case of a square array) are considered identical (as
in a Magic Square or Prime Array).
, a square array
results. Sometimes, the order of the elements in an array is significant (as in a Matrix), whereas at other times,
arrays which are equivalent modulo reflections (and rotations, in the case of a square array) are considered identical (as
in a Magic Square or Prime Array).
In order to exhaustively list the number of distinct arrays of a given shape with each element being one of ![]() possible
choices, the naive algorithm of running through each case and checking to see whether it's equivalent to an earlier one
is already just about as efficient as can be. The running time must be at least the number of answers, and this is so
close to
possible
choices, the naive algorithm of running through each case and checking to see whether it's equivalent to an earlier one
is already just about as efficient as can be. The running time must be at least the number of answers, and this is so
close to
![]() that the difference isn't significant.
that the difference isn't significant.
However, finding the number of possible arrays of a given shape is much easier, and an exact formula can be obtained using
the Polya Enumeration Theorem. For the simple case of an ![]() array, even this proves unnecessary since there
are only a few possible symmetry types, allowing the possibilities to be counted explicitly. For example, consider the case
of
array, even this proves unnecessary since there
are only a few possible symmetry types, allowing the possibilities to be counted explicitly. For example, consider the case
of ![]() and
and ![]() Even and distinct, so only reflections need be included. To take a specific case, let
Even and distinct, so only reflections need be included. To take a specific case, let ![]() and
and
![]() so the array looks like
so the array looks like
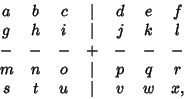
In general, it is therefore true that
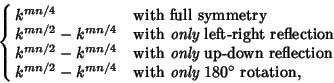
See also Antimagic Square, Euler Square, Kirkman's Schoolgirl Problem, Latin Rectangle, Latin Square, Magic Square, Matrix, Mrs. Perkins' Quilt, Multiplication Table, Orthogonal Array, Perfect Square, Prime Array, Quotient-Difference Table, Room Square, Stolarsky Array, Truth Table, Wythoff Array
|
|
|
© 1996-9 Eric W. Weisstein