|
|
|
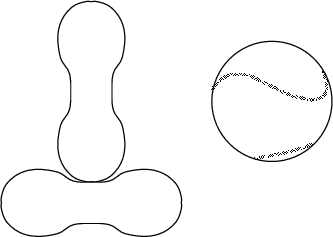
A pair of identical plane regions (mirror symmetric about two perpendicular lines through the center) which can be stitched together to form a baseball (or tennis ball). A baseball has a Circumference of 9 1/8 inches. The practical consideration of separating the regions far enough to allow the pitcher a good grip requires that the ``neck'' distance be about 1 3/16 inches. The baseball cover was invented by Elias Drake as a boy in the 1840s. (Thompson's attribution of the current design to trial and error development by C. H. Jackson in the 1860s is apparently unsubstantiated, as discovered by George Bart.)
One way to produce a baseball cover is to draw the regions on a Sphere, then cut them out. However, it is difficult to produce two identical regions in this manner. Thompson (1996) gives mathematical expressions giving baseball cover curves both in the plane and in 3-D. J. H. Conway has humorously proposed the following ``baseball curve conjecture:'' no two definitions of ``the'' baseball curve will give the same answer unless their equivalence was obvious from the start.
See also Baseball, Home Plate, Tennis Ball Theorem, Yin-Yang
References
Thompson, R. B. ``Designing a Baseball Cover. 1860's: Patience, Trial, and Error. 1990's: Geometry, Calculus, and
Computation.'' http://www.mathsoft.com/asolve/baseball/baseball.html. Rev. March 5, 1996.