|
|
|

A Cubic Ruled Surface (Fischer 1986) in which the director line meets the director Conic Section. Cayley's surface is the unique cubic surface having four Ordinary Double Points (Hunt), the maximum possible for Cubic Surface (Endraß). The Cayley cubic is invariant under the Tetrahedral Group and contains exactly nine lines, six of which connect the four nodes pairwise and the other three of which are coplanar (Endraß).
If the Ordinary Double Points in projective 3-space are taken as (1, 0, 0, 0), (0, 1, 0, 0),
(0, 0, 1, 0), (0, 0, 0, 1), then the equation of the surface in projective coordinates is
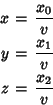

The Hessian of the Cayley cubic is given by
|
|
|
|
|
|
|
|
|
|
References
Endraß, S. ``Flächen mit vielen Doppelpunkten.'' DMV-Mitteilungen 4, 17-20, Apr. 1995.
Endraß, S. ``The Cayley Cubic.''
http://www.mathematik.uni-mainz.de/AlgebraischeGeometrie/docs/Ecayley.shtml.
Fischer, G. (Ed.). Mathematical Models from the Collections of Universities and Museums.
Braunschweig, Germany: Vieweg, p. 14, 1986.
Fischer, G. (Ed.). Plate 33 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, p. 33, 1986.
Hunt, B. ``Algebraic Surfaces.'' http://www.mathematik.uni-kl.de/~wwwagag/Galerie.html.
Hunt, B. The Geometry of Some Special Arithmetic Quotients. New York: Springer-Verlag, pp. 115-122, 1996.
Nordstrand, T. ``The Cayley Cubic.''
http://www.uib.no/people/nfytn/cleytxt.htm.
|
|
|
© 1996-9 Eric W. Weisstein