|
|
|
For three consecutive Orthogonal Polynomials
| (1) |
| (2) | |||
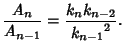 |
(3) |
| (4) |
| (5) |
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 785, 1972.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 42-44, 1975.