|
|
|
The downward Clenshaw recurrence formula evaluates a sum of products of indexed Coefficients by
functions which obey a recurrence relation. If
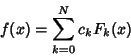
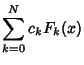 |
|||
The upward Clenshaw recurrence formula is
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Recurrence Relations and Clenshaw's
Recurrence Formula.'' §5.5 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 172-178, 1992.
|
|
|
© 1996-9 Eric W. Weisstein