Complete Graph

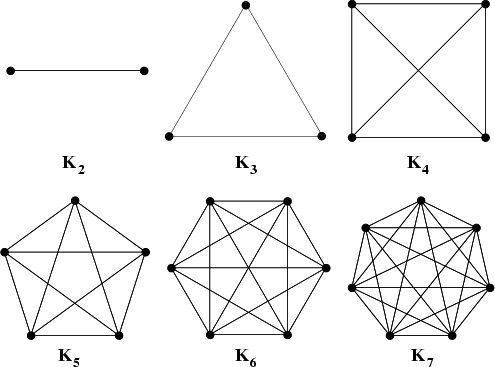
A Graph in which each pair of Vertices is connected by an Edge. The complete graph with $n$ Vertices is denoted $K_n$. In older literature, complete Graphs are called Universal Graphs.

$K_4$ is the Tetrahedral Graph and is therefore a Planar Graph. $K_5$ is nonplanar. Conway and Gordon (1983) proved that every embedding of $K_6$ is Intrinsically Linked with at least one pair of linked triangles. They also showed that any embedding of $K_7$ contains a knotted Hamiltonian Cycle.

The number of Edges in $K_v$ is $v(v-1)/2$, and the Genus is $(v-3)(v-4)/12$ for $v\geq 3$. The number of distinct variations for $K_n$ (Graphs which cannot be transformed into each other without passing nodes through an Edge or another node) for $n=1$, 2, ... are 1, 1, 1, 1, 1, 1, 6, 3, 411, 37, .... The Adjacency Matrix of the complete graph takes the particularly simple form of all 1s with 0s on the diagonal.

It is not known in general if a set of Trees with 1, 2, ..., $n-1$ Edges can always be packed into $K_n$. However, if the choice of Trees is restricted to either the path or star from each family, then the packing can always be done (Zaks and Liu 1977, Honsberger 1985).

References

Chartrand, G. Introductory Graph Theory. New York: Dover, pp. 29-30, 1985.

Conway, J. H. and Gordon, C. M. ``Knots and Links in Spatial Graphs.'' J. Graph Th. 7, 445-453, 1983.

Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 60-63, 1985.

Saaty, T. L. and Kainen, P. C. The Four-Color Problem: Assaults and Conquest. New York: Dover, p. 12, 1986.

Zaks, S. and Liu, C. L. ``Decomposition of Graphs into Trees.'' Proc. Eighth Southeastern Conference on Combinatorics, Graph Theory, and Computing. pp. 643-654, 1977.