|
|
|
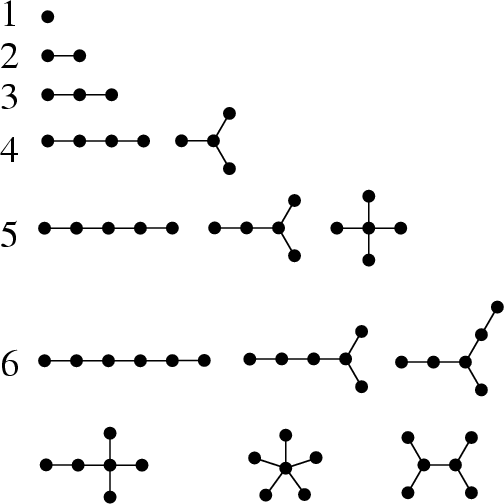
A tree is a mathematical structure which can be viewed as either a Graph or as a Data Structure. The two views are equivalent, since a tree Data Structure contains not only a set of elements, but also connections between elements, giving a tree graph.
A tree graph is a set of straight line segments connected at their ends containing no closed loops (cycles). A tree with ![]() nodes has
nodes has ![]() Edges. The points of connection are known as Forks and the segments
as Branches. Final segments and the nodes at their ends are called Leaves. A
tree with two Branches at each Fork and with one or two Leaves at the end
of each branch is called a Binary Tree.
Edges. The points of connection are known as Forks and the segments
as Branches. Final segments and the nodes at their ends are called Leaves. A
tree with two Branches at each Fork and with one or two Leaves at the end
of each branch is called a Binary Tree.
When a special node is designated to turn a tree into a Rooted Tree, it is called the Root (or sometimes ``Eve.'') In such a tree, each of the nodes which is one Edge further away from a given node is called a Child, and nodes connected to the same node which are the same distance from the Root are called Siblings.
Note that two Branches placed end-to-end are equivalent to a single Branch which means, for
example, that there is only one tree of order 3. The number ![]() of nonisomorphic trees of order
of nonisomorphic trees of order ![]() , 2,
... (where trees of orders 1, 2, ..., 6 are illustrated above), are 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, ...
(Sloane's A000055).
, 2,
... (where trees of orders 1, 2, ..., 6 are illustrated above), are 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, ...
(Sloane's A000055).
Otter showed that
| (1) |
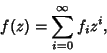 |
(2) |
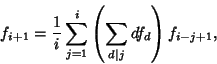 |
(3) |
| (4) |
| (5) |
![\begin{displaymath}
\beta={1\over\sqrt{2\pi}} \left[{1+\sum_{k=2}^\infty f'\left...
...pha_k}\right){1\over\alpha_k}}\right]^{3/2} = 0.5349485\ldots.
\end{displaymath}](t_1222.gif) |
(6) |
See also B-Tree, Binary Tree, Caterpillar Graph, Cayley Tree, Child, Dijkstra Tree, Eve, Forest, Kruskal's Algorithm, Kruskal's Tree Theorem, Leaf (Tree), Orchard-Planting Problem, Ordered Tree, Path Graph, Planted Planar Tree, Pólya Enumeration Theorem, Quadtree, Red-Black Tree, Root (Tree), Rooted Tree, Sibling, Star Graph, Stern-Brocot Tree, Weakly Binary Tree, Weighted Tree
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/otter/otter.html
Chauvin, B.; Cohen, S.; and Rouault, A. (Eds.). Trees: Workshop in Versailles, June 14-16, 1995.
Basel, Switzerland: Birkhäuser, 1996.
Gardner, M. ``Trees.'' Ch. 17 in
Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American.
New York: Vintage, pp. 240-250, 1978.
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, 1994.
Harary, F. and Manvel, B. ``Trees.'' Scripta Math. 28, 327-333, 1970.
Harary, F. and Palmer, E. M. Graphical Enumeration. New York: Academic Press, 1973.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973.
Otter, R. ``The Number of Trees.'' Ann. Math. 49, 583-599, 1948.
Sloane, N. J. A. Sequence
A000055/M0791
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in
Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
|
|
|
© 1996-9 Eric W. Weisstein