Concave

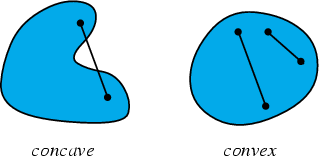
$\begin{figure}\begin{center}\BoxedEPSF{ConcaveConvex.epsf}\end{center}\end{figure}$

A Set in $\Bbb{R}^d$ is concave if it does not contain all the Line Segments connecting any pair of its points. If the Set does contain all the Line Segments, it is called Convex.

See also Connected Set, Convex Function, Convex Hull, Convex Optimization Theory, Convex Polygon, Delaunay Triangulation, Simply Connected