The probability that a measurement will fall within a given Closed Interval ![$[a,b]$](c2_471.gif) . For a continuous distribution,
. For a continuous distribution,
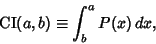 |
(1) |
where 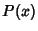 is the Probability Distribution Function. Usually, the confidence interval of interest is
symmetrically placed around the mean, so
is the Probability Distribution Function. Usually, the confidence interval of interest is
symmetrically placed around the mean, so
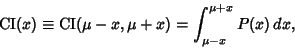 |
(2) |
where  is the Mean. For a Gaussian Distribution, the probability that a measurement falls within
is the Mean. For a Gaussian Distribution, the probability that a measurement falls within
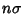 of the mean
of the mean  is
is
Now let
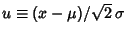 , so
, so
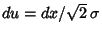 . Then
. Then
where
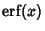 is the so-called Erf function. The variate value producing a confidence interval CI is often denoted
is the so-called Erf function. The variate value producing a confidence interval CI is often denoted
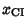 , so
, so
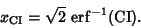 |
(5) |
| range |
CI |
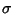 |
0.6826895 |
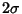 |
0.9544997 |
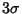 |
0.9973002 |
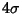 |
0.9999366 |
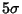 |
0.9999994 |
To find the standard deviation range corresponding to a given confidence interval, solve (4) for 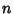 .
.
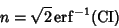 |
(6) |
| CI |
range |
| 0.800 |
± 1.28155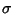 |
| 0.900 |
± 1.64485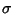 |
| 0.950 |
± 1.95996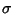 |
| 0.990 |
± 2.57583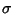 |
| 0.995 |
± 2.80703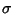 |
| 0.999 |
± 3.29053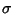 |
© 1996-9 Eric W. Weisstein
1999-05-26
![]() . For a continuous distribution,
. For a continuous distribution,
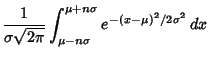
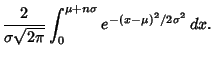
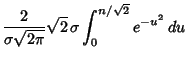
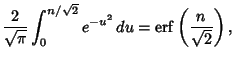
![]() .
.