The ``error function'' encountered in integrating the Gaussian Distribution.
where Erfc is the complementary error function and 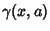 is the incomplete Gamma Function. It can
also be defined as a Maclaurin Series
is the incomplete Gamma Function. It can
also be defined as a Maclaurin Series
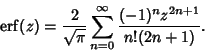 |
(4) |
Erf has the values
It is an Odd Function
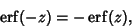 |
(7) |
and satisfies
 |
(8) |
Erf may be expressed in terms of a Confluent Hypergeometric Function of the First Kind 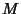 as
as
 |
(9) |
Erf is bounded by
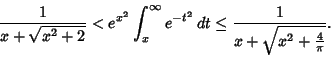 |
(10) |
Its Derivative is
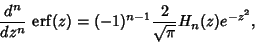 |
(11) |
where 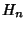 is a Hermite Polynomial. The first Derivative is
is a Hermite Polynomial. The first Derivative is
 |
(12) |
and the integral is
 |
(13) |
For 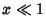 , erf may be computed from
, erf may be computed from
(Acton 1990). For  ,
,
Using Integration by Parts gives
so
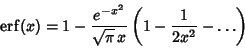 |
(20) |
and continuing the procedure gives the Asymptotic Series
 |
(21) |
A Complex generalization of
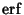 is defined as
is defined as
See also Dawson's Integral,
Erfc, Erfi, Gaussian Integral, Normal Distribution Function, Probability Integral
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Error Function'' and ``Repeated Integrals of the Error Function.''
§7.1-7.2 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 297-300, 1972.
Acton, F. S. Numerical Methods That Work, 2nd printing. Washington, DC: Math. Assoc. Amer., p. 16, 1990.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 568-569, 1985.
Spanier, J. and Oldham, K. B. ``The Error Function
 and Its Complement
and Its Complement
 .''
Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
.''
Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
© 1996-9 Eric W. Weisstein
1999-05-25
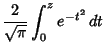
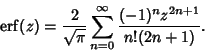
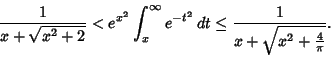
![]() , erf may be computed from
, erf may be computed from
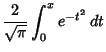
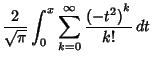
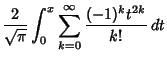
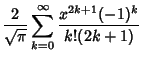
![$\displaystyle {2\over\sqrt{\pi}} e^{-x^2}x \left[{1+{2x^2\over 1\cdot 3}+{(2x)^2\over 1\cdot 3\cdot 5}+\ldots}\right]$](e_1689.gif)
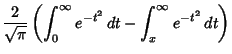
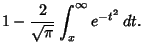

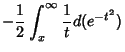
![$\displaystyle -{1\over 2}\left[{e^{-t^2}\over t}\right]^\infty_x -{1\over 2}\int_x^\infty {e^{-t^2}\,dt\over t^2}$](e_1695.gif)
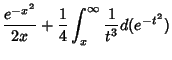
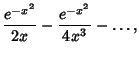
![]() is defined as
is defined as
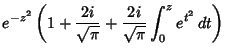
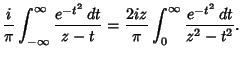
![]() and Its Complement
and Its Complement
![]() .''
Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.
.''
Ch. 40 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393, 1987.