|
|
|
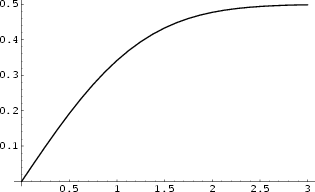
A normalized form of the cumulative Gaussian Distribution function giving the probability that a variate
assumes a value in the range ![]() ,
,
| (1) |
| (2) |
| (3) |
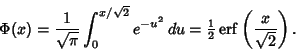 |
(4) |
| (5) |
Note that a function different from ![]() is sometimes defined as ``the'' normal distribution function
is sometimes defined as ``the'' normal distribution function
| (6) |
The value of ![]() for which
for which ![]() falls within the interval
falls within the interval ![]() with a given probability
with a given probability ![]() is a related quantity
called the Confidence Interval.
is a related quantity
called the Confidence Interval.
For small values ![]() , a good approximation to
, a good approximation to ![]() is obtained from the Maclaurin Series for Erf,
is obtained from the Maclaurin Series for Erf,
| (7) |
| (8) |
 |
(9) |
 |
(10) |
| (11) |

The first Quartile of a standard Normal Distribution occurs when
| (12) |
See also Confidence Interval, Erf, Erfc, Fisher-Behrens Problem, Gaussian Distribution, Gaussian Integral, Hh Function, Normal Distribution, Probability Integral, Tetrachoric Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 931-933, 1972.
Bagby, R. J. ``Calculating Normal Probabilities.'' Amer. Math. Monthly 102, 46-49, 1995.
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, 1987.
Johnson, N.; Kotz, S.; and Balakrishnan, N. Continuous Univariate Distributions, Vol. 1, 2nd ed. Boston, MA: Houghton Mifflin, 1994.
|
|
|
© 1996-9 Eric W. Weisstein