For two variables 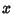 and
and 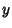 ,
,
 |
(1) |
where 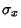 denotes Standard Deviation and
denotes Standard Deviation and
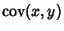 is the Covariance of these two variables. For
the general case of variables
is the Covariance of these two variables. For
the general case of variables 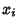 and
and 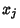 , where
, where 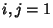 , 2, ...,
, 2, ..., 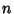 ,
,
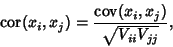 |
(2) |
where 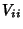 are elements of the Covariance Matrix. In general, a correlation gives the strength of the
relationship between variables. The variance of any quantity is alway Nonnegative by
definition, so
are elements of the Covariance Matrix. In general, a correlation gives the strength of the
relationship between variables. The variance of any quantity is alway Nonnegative by
definition, so
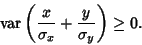 |
(3) |
From a property of Variances, the sum can be expanded
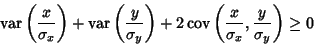 |
(4) |
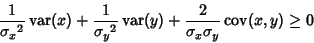 |
(5) |
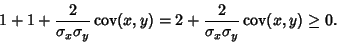 |
(6) |
Therefore,
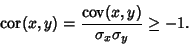 |
(7) |
Similarly,
 |
(8) |
 |
(9) |
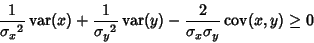 |
(10) |
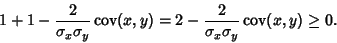 |
(11) |
Therefore,
 |
(12) |
so
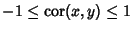 . For a linear combination of two variables,
. For a linear combination of two variables,
Examine the cases where
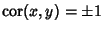 ,
,
 |
(14) |
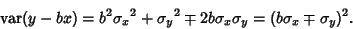 |
(15) |
The Variance will be zero if
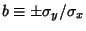 , which requires that the argument of the
Variance is a constant. Therefore,
, which requires that the argument of the
Variance is a constant. Therefore, 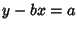 , so
, so 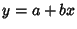 . If
. If
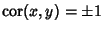 ,
, 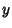 is either perfectly
correlated (
is either perfectly
correlated (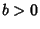 ) or perfectly anticorrelated (
) or perfectly anticorrelated (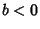 ) with
) with 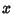 .
.
See also Covariance, Covariance Matrix, Variance
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() ,
,