|
|
|
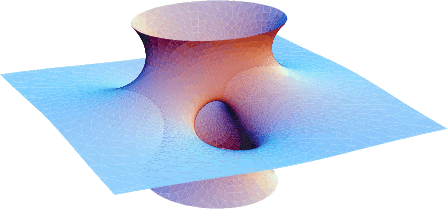
A complete embedded Minimal Surface of finite topology. It has no Boundary and does not intersect itself. It can be represented parametrically by
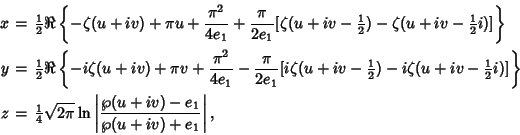
References
Costa, A. ``Examples of a Complete Minimal Immersion in
do Carmo, M. P.
Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer).
Braunschweig, Germany: Vieweg, p. 43, 1986.
Gray, A. Modern Differential Geometry of Curves and Surfaces.Boca Raton, FL: CRC Press, 1993.
Gray, A. Images of the Costa surface. ftp://bianchi.umd.edu/pub/COSTAPS/.
Nordstrand, T. ``Costa-Hoffman-Meeks Minimal Surface.''
http://www.uib.no/people/nfytn/costatxt.htm.
Peterson, I. ``The Song in the Stone: Developing the Art of Telecarving a Minimal Surface.'' Sci. News
149, 110-111, Feb. 17, 1996.
![]() of Genus One and Three Embedded Ends.''
Bil. Soc. Bras. Mat. 15, 47-54, 1984.
of Genus One and Three Embedded Ends.''
Bil. Soc. Bras. Mat. 15, 47-54, 1984.