|
|
|
The point on the Positive Ray of the Normal Vector at a distance ![]() , where
, where ![]() is the Radius
of Curvature. It is given by
is the Radius
of Curvature. It is given by
| (1) |
| (2) |
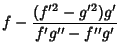 |
(3) | ||
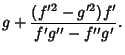 |
(4) |
References
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, 1993.