|
|
|
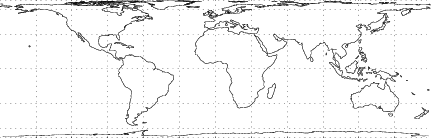
The Map Projection having transformation equations,
| (1) | |||
| (2) |
| (3) | |||
| (4) |
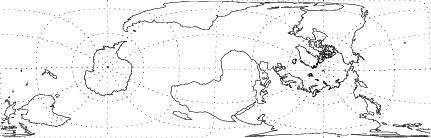
An oblique form of the cylindrical equal-area projection is given by the equations
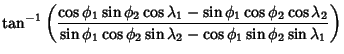 |
|||
| (5) | |||
![$\displaystyle \tan^{-1}\left[{-{\cos(\lambda_p-\lambda_1)\over\tan\phi_1}}\right],$](c4_1181.gif) |
(6) |
| (7) | |||
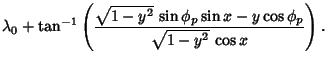 |
|||
| (8) |
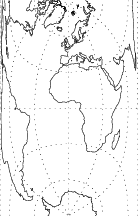
A transverse form of the cylindrical equal-area projection is given by the equations
| (9) | |||
![$\displaystyle \tan^{-1}\left[{\tan\phi\over\cos(\lambda-\lambda_0)}\right]-\phi_0,$](c4_1186.gif) |
(10) |
| (11) | |||
![$\displaystyle \lambda_0+\tan^{-1}\left[{{x\over\sqrt{1-x^2}}\cos(y+\phi_0)}\right].$](c4_1188.gif) |
(12) |
References
Snyder, J. P. Map Projections--A Working Manual. U. S. Geological Survey Professional Paper 1395. Washington,
DC: U. S. Government Printing Office, pp. 76-85, 1987.
|
|
|
© 1996-9 Eric W. Weisstein