Define the  matrices
matrices
where
 are the Pauli Matrices, I is the Identity Matrix,
are the Pauli Matrices, I is the Identity Matrix,  , 2, 3, and
, 2, 3, and
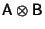 is the matrix Direct Product. Explicitly,
is the matrix Direct Product. Explicitly,
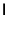 |
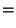 |
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right]$](d2_11.gif) |
(3) |
 |
 |
![$\displaystyle \left[\begin{array}{cccc}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{array}\right]$](d2_13.gif) |
(4) |
 |
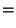 |
![$\displaystyle \left[\begin{array}{cccc}0 & -i & 0 & 0\\ i & 0 & 0 & 0\\ 0 & 0 & 0 & -i\\ 0 & 0 & i & 0\end{array}\right]$](d2_15.gif) |
(5) |
 |
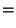 |
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\end{array}\right]$](d2_17.gif) |
(6) |
 |
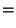 |
![$\displaystyle \left[\begin{array}{cccc}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{array}\right]$](d2_19.gif) |
(7) |
 |
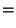 |
![$\displaystyle \left[\begin{array}{cccc}0 & 0 & -i & 0\\ 0 & 0 & 0 & -i\\ i & 0 & 0 & 0\\ 0 & i & 0 & 0\end{array}\right]$](d2_21.gif) |
(8) |
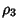 |
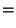 |
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array}\right].$](d2_23.gif) |
(9) |
These matrices satisfy the anticommutation identities
 |
(10) |
 |
(11) |
where  is the Kronecker Delta, the commutation identity
is the Kronecker Delta, the commutation identity
![\begin{displaymath}[\sigma_i, \rho_j]=\sigma_i\rho_j-\rho_j\sigma_i=0,
\end{displaymath}](d2_27.gif) |
(12) |
and are cyclic under permutations of indices
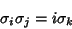 |
(13) |
 |
(14) |
A total of 16 Dirac matrices can be defined via
 |
(15) |
for  , 1, 2, 3 and where
, 1, 2, 3 and where
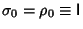 . These matrices satisfy
. These matrices satisfy
- 1.
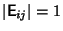 , where
, where
 is the Determinant,
is the Determinant,
- 2.
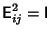 ,
,
- 3.
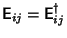 , making them Hermitian, and therefore unitary,
, making them Hermitian, and therefore unitary,
- 4.
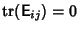 , except
, except
 ,
,
- 5. Any two
 multiplied together yield a Dirac matrix to within a multiplicative factor of
multiplied together yield a Dirac matrix to within a multiplicative factor of 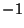 or
or  ,
,
- 6. The
 are linearly independent,
are linearly independent,
- 7. The
 form a complete set, i.e., any
form a complete set, i.e., any  constant matrix may be written as
constant matrix may be written as
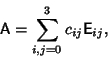 |
(16) |
where the 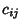 are real or complex and are given by
are real or complex and are given by
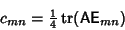 |
(17) |
(Arfken 1985).
Dirac's original matrices were written  and were defined by
and were defined by
for  , 2, 3, giving
, 2, 3, giving
The additional matrix
![\begin{displaymath}
\alpha_5={\hbox{\sf E}}_{20}=\rho_2=\left[{\matrix{0 & 0 & -...
...r 0 & 0 & 0 & -i\cr i & 0 & 0 & 0\cr 0 & i & 0 & 0\cr}}\right]
\end{displaymath}](d2_57.gif) |
(24) |
is sometimes defined. Other sets of Dirac matrices are sometimes defined as
and
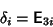 |
(28) |
for  , 2, 3 (Arfken 1985) and
, 2, 3 (Arfken 1985) and
for  , 2, 3 (Goldstein 1980).
, 2, 3 (Goldstein 1980).
Any of the 15 Dirac matrices (excluding the identity matrix) commute with eight Dirac matrices and anticommute with the
other eight. Let
 , then
, then
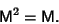 |
(31) |
In addition
![\begin{displaymath}
\left[{\matrix{\alpha_1\cr \alpha_2\cr \alpha_3\cr}}\right]\...
...\matrix{\alpha_1\cr \alpha_2\cr \alpha_3\cr}}\right]=2i\sigma.
\end{displaymath}](d2_71.gif) |
(32) |
The products of  and
and 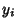 satisfy
satisfy
 |
(33) |
 |
(34) |
The 16 Dirac matrices form six anticommuting sets of five matrices each:
- 1.
 ,
, 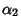 ,
, 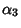 ,
, 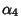 ,
, 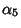 ,
,
- 2.
 ,
,  ,
, 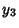 ,
,  ,
, 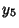 ,
,
- 3.
 ,
,  ,
,  ,
,  ,
, 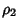 ,
,
- 4.
 ,
,  ,
,  ,
,  ,
,  ,
,
- 5.
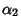 ,
,  ,
,  ,
,  ,
,  ,
,
- 6.
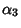 ,
, 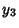 ,
,  ,
,  ,
,  .
.
See also Pauli Matrices
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 211-213, 1985.
Goldstein, H. Classical Mechanics, 2nd ed. Reading, MA: Addison-Wesley, p. 580, 1980.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() matrices
matrices
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\end{array}\right]$](d2_11.gif)
![$\displaystyle \left[\begin{array}{cccc}0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\end{array}\right]$](d2_13.gif)
![$\displaystyle \left[\begin{array}{cccc}0 & -i & 0 & 0\\ i & 0 & 0 & 0\\ 0 & 0 & 0 & -i\\ 0 & 0 & i & 0\end{array}\right]$](d2_15.gif)
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\end{array}\right]$](d2_17.gif)
![$\displaystyle \left[\begin{array}{cccc}0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\end{array}\right]$](d2_19.gif)
![$\displaystyle \left[\begin{array}{cccc}0 & 0 & -i & 0\\ 0 & 0 & 0 & -i\\ i & 0 & 0 & 0\\ 0 & i & 0 & 0\end{array}\right]$](d2_21.gif)
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array}\right].$](d2_23.gif)
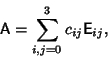
![]() and were defined by
and were defined by
![$\displaystyle {\hbox{\sf E}}_{11}=\left[\begin{array}{cccc}0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\end{array}\right]$](d2_51.gif)
![$\displaystyle {\hbox{\sf E}}_{12}=\left[\begin{array}{cccc}0 & 0 & 0 & -i\\ 0 & 0 & i & 0\\ 0 & -i & 0 & 0\\ i & 0 & 0 & 0\end{array}\right]$](d2_53.gif)
![$\displaystyle {\hbox{\sf E}}_{13}=\left[\begin{array}{cccc}0 & 0 & 1 & 0\\ 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0\\ 0 & -1 & 0 & 0\end{array}\right]$](d2_55.gif)
![$\displaystyle {\hbox{\sf E}}_{30}=\left[\begin{array}{cccc}1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array}\right].$](d2_56.gif)
![\begin{displaymath}
\alpha_5={\hbox{\sf E}}_{20}=\rho_2=\left[{\matrix{0 & 0 & -...
...r 0 & 0 & 0 & -i\cr i & 0 & 0 & 0\cr 0 & i & 0 & 0\cr}}\right]
\end{displaymath}](d2_57.gif)
![$\displaystyle \left[\begin{array}{cc}{\hbox{\sf0}} & \sigma_i\\ -\sigma_i & {\hbox{\sf0}}\end{array}\right]$](d2_66.gif)
![$\displaystyle \left[\begin{array}{cc}{\hbox{\sf I}}& {\hbox{\sf0}}\\ 2{\hbox{\sf I}}& -{\hbox{\sf I}}\end{array}\right]$](d2_68.gif)
![]() , then
, then
![\begin{displaymath}
\left[{\matrix{\alpha_1\cr \alpha_2\cr \alpha_3\cr}}\right]\...
...\matrix{\alpha_1\cr \alpha_2\cr \alpha_3\cr}}\right]=2i\sigma.
\end{displaymath}](d2_71.gif)