For a first-Rank Tensor (i.e., a Vector),
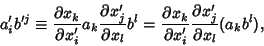 |
(1) |
which is a second-Rank Tensor. The Contraction of a
direct product of first-Rank Tensors is the Scalar
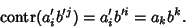 |
(2) |
For a second-Rank Tensor,
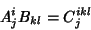 |
(3) |
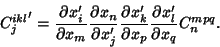 |
(4) |
For a general Tensor, the direct product of two Tensors is
a Tensor of Rank equal to the sum of
the two initial Ranks. The direct product is Associative, but not Commutative.
References
Arfken, G. ``Contraction, Direct Product.'' §3.2 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 124-126, 1985.
© 1996-9 Eric W. Weisstein
1999-05-24