|
|
|
Let Jones and Smith be the only two contestants in an election that will end in a
deadlock when all votes for Jones (![]() ) and Smith (
) and Smith (![]() ) are counted.
What is the Expectation Value of
) are counted.
What is the Expectation Value of
![]() after
after ![]() votes are counted? The solution is
votes are counted? The solution is
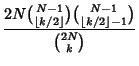 |
|||
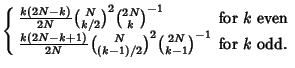 |
References
Handelsman, M. B. Solution to Problem 10248. ``Early Returns in a Tied Election.'' Amer. Math. Monthly 102, 554-556, 1995.