|
|
|
The elementary symmetric functions ![]() on
on ![]() variables
variables
![]() are defined by
are defined by
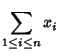 |
(1) | ||
 |
(2) | ||
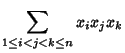 |
(3) | ||
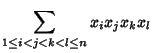 |
(4) | ||
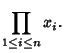 |
(5) |
| (6) |
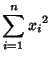 |
(7) | ||
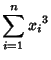 |
(8) | ||
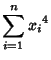 |
(9) |
See also Fundamental Theorem of Symmetric Functions, Newton's Relations, Symmetric Function
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.