|
|
|
A Maximum or Minimum. An extremum may be Local (a.k.a. a Relative Extremum; an
extremum in a given region which is not the overall Maximum or Minimum) or Global.
Functions with many extrema can be very difficult to Graph. Notorious examples include the
functions ![]() and
and ![]() near
near ![]()
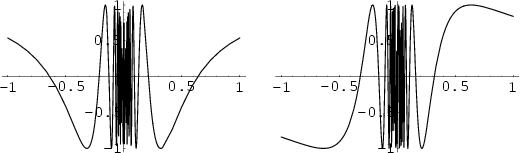
and
![]() near 0 and 1.
near 0 and 1.

The latter has
See also Global Extremum, Global Maximum, Global Minimum, Kuhn-Tucker Theorem, Lagrange Multiplier, Local Extremum, Local Maximum, Local Minimum, Maximum, Minimum
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 14, 1972.
Mulcahy, C. ``Plotting and Scheming with Wavelets.'' Math. Mag. 69, 323-343, 1996.
Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.