|
|
|
The smallest value of a set, function, etc. The minimum value of a set of elements
![]() is denoted
is denoted ![]() or
or
![]() , and is equal to the first element of a sorted (i.e., ordered) version of
, and is equal to the first element of a sorted (i.e., ordered) version of ![]() . For example, given the set
. For example, given the set ![]() 3,
5, 4, 1
3,
5, 4, 1![]() , the sorted version is
, the sorted version is ![]() 1, 3, 4, 5
1, 3, 4, 5![]() , so the minimum is 1. The Maximum and minimum are the simplest
Order Statistics.
, so the minimum is 1. The Maximum and minimum are the simplest
Order Statistics.
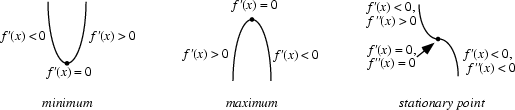
A continuous Function may assume a minimum at a single point or may have minima at a number of points. A Global Minimum of a Function is the smallest value in the entire Range of the Function, while a Local Minimum is the smallest value in some local neighborhood.
For a function ![]() which is Continuous at a point
which is Continuous at a point ![]() , a Necessary but not
Sufficient condition for
, a Necessary but not
Sufficient condition for ![]() to have a Relative Minimum at
to have a Relative Minimum at ![]() is that
is that ![]() be a Critical
Point (i.e.,
be a Critical
Point (i.e., ![]() is either not Differentiable at
is either not Differentiable at ![]() or
or ![]() is a Stationary Point, in which case
is a Stationary Point, in which case
![]() ).
).
The First Derivative Test can be applied to Continuous Functions to distinguish minima
from Maxima. For twice differentiable functions of one variable, ![]() , or of two variables,
, or of two variables, ![]() ,
the Second Derivative Test can sometimes also identify the nature of an Extremum. For a function
,
the Second Derivative Test can sometimes also identify the nature of an Extremum. For a function ![]() , the
Extremum Test succeeds under more general conditions than the Second Derivative Test.
, the
Extremum Test succeeds under more general conditions than the Second Derivative Test.
See also Critical Point, Extremum, First Derivative Test, Global Maximum, Inflection Point, Local Maximum, Maximum, Midrange, Order Statistic, Saddle Point (Function), Second Derivative Test, Stationary Point
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 14, 1972.
Brent, R. P. Algorithms for Minimization Without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.
Nash, J. C. ``Descent to a Minimum I-II: Variable Metric Algorithms.''
Chs. 15-16 in Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation, 2nd ed.
Bristol, England: Adam Hilger, pp. 186-206, 1990.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Minimization or Maximization of Functions.''
Ch. 10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 387-448, 1992.
Tikhomirov, V. M. Stories About Maxima and Minima. Providence, RI: Amer. Math. Soc., 1991.
|
|
|
© 1996-9 Eric W. Weisstein