A Point of a Function or Surface which is a Stationary Point but not an Extremum.
An example of a 1-D Function with a saddle point is 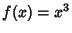 , which has
, which has
This function has a saddle point at  by the Extremum Test since
by the Extremum Test since  and
and
 .
An example of a Surface with a saddle point is the Monkey Saddle.
.
An example of a Surface with a saddle point is the Monkey Saddle.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , which has
, which has