|
|
|
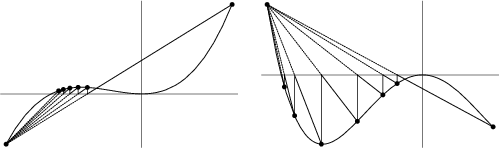
An Algorithm for finding Roots which uses the point where the linear approximation crosses the
axis as the next iteration and keeps the same initial point for each iteration. Using the two-point form of the line
See also Brent's Method, Ridders' Method, Secant Method
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 18, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Secant Method, False Position Method,
and Ridders' Method.'' §9.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 347-352, 1992.