If  is Normally Distributed with Mean
is Normally Distributed with Mean 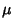 and Variance
and Variance 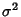 , then
a linear function of
, then
a linear function of  ,
,
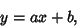 |
(1) |
is also Normally Distributed. The new distribution has Mean 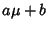 and
Variance
and
Variance 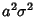 , as can be derived using the Moment-Generating Function
, as can be derived using the Moment-Generating Function
which is of the standard form with
 |
(3) |
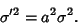 |
(4) |
For a weighted sum of independent variables
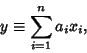 |
(5) |
the expectation is given by
Setting this equal to
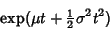 |
(7) |
gives
Therefore, the Mean and Variance of the weighted sums of  Random Variables
are their weighted sums.
Random Variables
are their weighted sums.
If 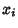 are Independent and Normally Distributed with
Mean 0 and Variance
are Independent and Normally Distributed with
Mean 0 and Variance 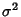 , define
, define
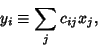 |
(10) |
where 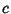 obeys the Orthogonality Condition
obeys the Orthogonality Condition
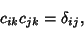 |
(11) |
with 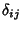 the Kronecker Delta. Then
the Kronecker Delta. Then 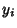 are also independent and normally distributed with Mean 0
and Variance
are also independent and normally distributed with Mean 0
and Variance 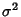 .
.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() is Normally Distributed with Mean
is Normally Distributed with Mean ![]() and Variance
and Variance ![]() , then
a linear function of
, then
a linear function of ![]() ,
,
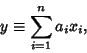

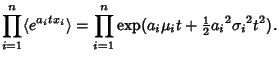
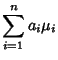
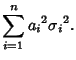
![]() are Independent and Normally Distributed with
Mean 0 and Variance
are Independent and Normally Distributed with
Mean 0 and Variance ![]() , define
, define