A Partial Differential Equation of second-order, i.e., one of the form
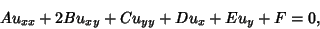 |
(1) |
is called hyperbolic if the Matrix
![\begin{displaymath}
{\hbox{\sf Z}} \equiv \left[{\matrix{A & B\cr B & C\cr}}\right]
\end{displaymath}](h_2131.gif) |
(2) |
satisfies det
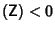 . The Wave Equation is an example of a hyperbolic partial differential equation.
Initial-boundary conditions are used to give
. The Wave Equation is an example of a hyperbolic partial differential equation.
Initial-boundary conditions are used to give
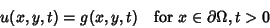 |
(3) |
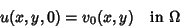 |
(4) |
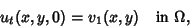 |
(5) |
where
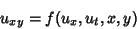 |
(6) |
holds in 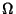 .
.
See also Elliptic Partial Differential Equation, Parabolic Partial Differential Equation,
Partial Differential Equation
© 1996-9 Eric W. Weisstein
1999-05-25