The wave equation is
 |
(1) |
where 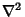 is the Laplacian.
is the Laplacian.
The 1-D wave equation is
 |
(2) |
In order to specify a wave, the equation is subject to boundary conditions
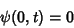 |
(3) |
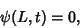 |
(4) |
and initial conditions
The wave equation can be solved using the so-called d'Alembert's solution, a Fourier Transform method, or
Separation of Variables.
d'Alembert  devised his solution in 1746, and Euler
devised his solution in 1746, and Euler  subsequently expanded the method in 1748. Let
subsequently expanded the method in 1748. Let
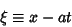 |
(7) |
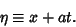 |
(8) |
By the Chain Rule,
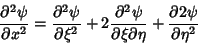 |
(9) |
 |
(10) |
The wave equation then becomes
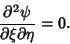 |
(11) |
Any solution of this equation is of the form
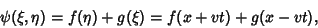 |
(12) |
where 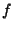 and
and 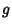 are any functions. They represent two waveforms traveling in opposite directions,
are any functions. They represent two waveforms traveling in opposite directions, 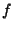 in the
Negative
in the
Negative 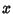 direction and
direction and 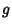 in the Positive
in the Positive 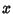 direction.
direction.
The 1-D wave equation can also be solved by applying a Fourier Transform to each side,
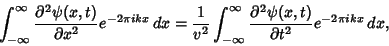 |
(13) |
which is given, with the help of the Fourier Transform Derivative identity, by
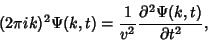 |
(14) |
where
![\begin{displaymath}
\Psi(k,t) \equiv {\mathcal F}[\psi(x,t)] = \int_{-\infty}^\infty \psi(x,t)e^{-2\pi ikx}\,dx.
\end{displaymath}](w_165.gif) |
(15) |
This has solution
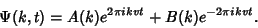 |
(16) |
Taking the inverse Fourier Transform gives
where
![\begin{displaymath}
f_1(u)\equiv {\mathcal F}[A(k)] = \int_{-\infty}^\infty A(k)e^{-2\pi iku}\,dk
\end{displaymath}](w_172.gif) |
(18) |
![\begin{displaymath}
f_2(u)\equiv {\mathcal F}[B(k)] = \int_{-\infty}^\infty B(k)e^{-2\pi iku}\,dk.
\end{displaymath}](w_173.gif) |
(19) |
This solution is still subject to all other initial and boundary conditions.
The 1-D wave equation can be solved by Separation of Variables using a trial solution
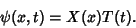 |
(20) |
This gives
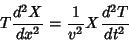 |
(21) |
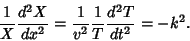 |
(22) |
So the solution for 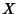 is
is
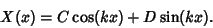 |
(23) |
Rewriting (22) gives
 |
(24) |
so the solution for 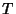 is
is
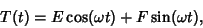 |
(25) |
where
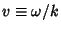 . Applying the boundary conditions
. Applying the boundary conditions
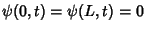 to (23) gives
to (23) gives
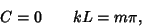 |
(26) |
where 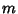 is an Integer. Plugging (23), (25) and (26) back in for
is an Integer. Plugging (23), (25) and (26) back in for 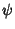 in (21) gives, for a
particular value of
in (21) gives, for a
particular value of 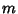 ,
,
The initial condition
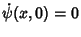 then gives
then gives 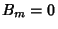 , so (27) becomes
, so (27) becomes
 |
(28) |
The general solution is a sum over all possible values of 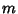 , so
, so
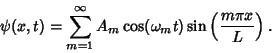 |
(29) |
Using Orthogonality of sines again,
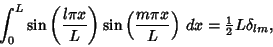 |
(30) |
where 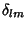 is the Kronecker Delta defined by
is the Kronecker Delta defined by
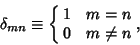 |
(31) |
gives
so we have
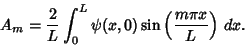 |
(33) |
The computation of 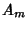 s for specific initial distortions is derived in the Fourier Sine Series section. We already have found
that
s for specific initial distortions is derived in the Fourier Sine Series section. We already have found
that 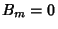 , so the equation of motion for the string (29), with
, so the equation of motion for the string (29), with
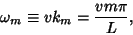 |
(34) |
is
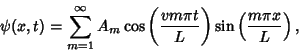 |
(35) |
where the 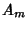 Coefficients are given by (33).
Coefficients are given by (33).
A damped 1-D wave
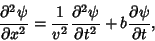 |
(36) |
given boundary conditions
initial conditions
and the additional constraint
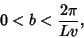 |
(41) |
can also be solved as a Fourier Series.
![\begin{displaymath}
\psi(x,t) = \sum_{n=1}^\infty \sin\left({n\pi x\over L}\right)e^{-v^2bt/2} [a_n\sin(\mu_nt)+b_n\cos(\mu_nt)],
\end{displaymath}](w_211.gif) |
(42) |
where
To find the motion of a rectangular membrane with sides of length 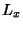 and
and  (in the absence of
gravity
(in the absence of
gravity  ), use the 2-D wave equation
), use the 2-D wave equation
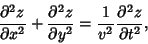 |
(46) |
where 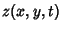 is the vertical displacement of a point on the membrane at position (
is the vertical displacement of a point on the membrane at position (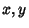 ) and time
) and time 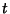 . Use
Separation of Variables to look for solutions of the form
. Use
Separation of Variables to look for solutions of the form
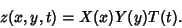 |
(47) |
Plugging (47) into (46) gives
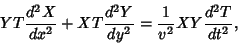 |
(48) |
where the partial derivatives have now become complete derivatives. Multiplying (48) by  gives
gives
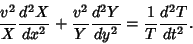 |
(49) |
The left and right sides must both be equal to a constant, so we can separate the equation by writing the right side as
 |
(50) |
This has solution
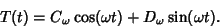 |
(51) |
Plugging (50) back into (49),
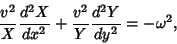 |
(52) |
which we can rewrite as
 |
(53) |
since the left and right sides again must both be equal to a constant. We can now separate out the 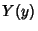 equation
equation
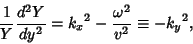 |
(54) |
where we have defined a new constant 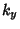 satisfying
satisfying
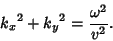 |
(55) |
Equations (53) and (54) have solutions
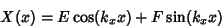 |
(56) |
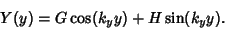 |
(57) |
We now apply the boundary conditions to (56) and (57). The conditions 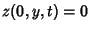 and
and 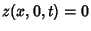 mean that
mean that
 |
(58) |
Similarly, the conditions 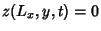 and
and 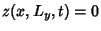 give
give
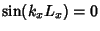 and
and
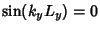 , so
, so 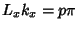 and
and 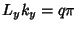 , where
, where 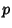 and
and 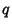 are Integers. Solving for the allowed values of
are Integers. Solving for the allowed values of 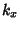 and
and 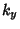 then gives
then gives
 |
(59) |
Plugging (52), (56), (57), (58), and (59) back into (22) gives the solution for particular
values of 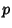 and
and 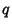 ,
,
![\begin{displaymath}
z_{pq}(x,y,t) = [C_\omega\cos(\omega t)+D_\omega\sin(\omega ...
...)}\right]\left[{H_q\sin\left({q\pi y\over L_y}\right)}\right].
\end{displaymath}](w_251.gif) |
(60) |
Lumping the constants together by writing
 (we can do this since
(we can do this since 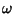 is a function of
is a function of
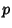 and
and 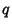 , so
, so 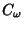 can be written as
can be written as 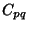 ) and
) and
 , we obtain
, we obtain
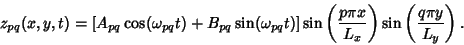 |
(61) |
Plots of the spatial part for modes (1, 1), (1, 2), (2, 1), and (2, 2) follow.
The general solution is a sum over all possible values of 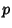 and
and 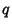 , so the final solution is
, so the final solution is
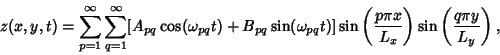 |
(62) |
where 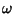 is defined by combining (55) and (59) to yield
is defined by combining (55) and (59) to yield
 |
(63) |
Given the initial conditions 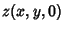 and
and
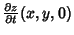 , we can compute the
, we can compute the 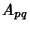 s and
s and
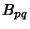 s explicitly. To accomplish this, we make use of the orthogonality of the Sine function in the form
s explicitly. To accomplish this, we make use of the orthogonality of the Sine function in the form
 |
(64) |
where 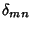 is the Kronecker Delta.
This can be demonstrated by direct Integration. Let
is the Kronecker Delta.
This can be demonstrated by direct Integration. Let
 so
so
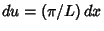 in (64), then
in (64), then
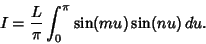 |
(65) |
Now use the trigonometric identity
![\begin{displaymath}
\sin\alpha\sin\beta ={\textstyle{1\over 2}}[\cos(\alpha-\beta)-\cos(\alpha+\beta)]
\end{displaymath}](w_270.gif) |
(66) |
to write
![\begin{displaymath}
I = {L\over 2\pi} \int_0^\pi \cos[(m-n)u]\,du+\int_0^\pi \cos [(m+n)u]\,du.
\end{displaymath}](w_271.gif) |
(67) |
Note that for an Integer 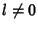 , the following Integral vanishes
, the following Integral vanishes
since 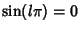 when
when  is an Integer. Therefore,
is an Integer. Therefore, 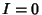 when
when
 . However,
. However, 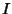 does not
vanish when
does not
vanish when 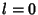 , since
, since
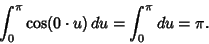 |
(69) |
We therefore have that
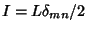 , so we have derived (64). Now we multiply
, so we have derived (64). Now we multiply 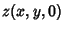 by two sine
terms and integrate between 0 and
by two sine
terms and integrate between 0 and 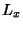 and between 0 and
and between 0 and  ,
,
![\begin{displaymath}
I=\int_0^{L_y}\left[{\int_0^{L_x} z(x,y,0)\sin\left({p\pi x\...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_284.gif) |
(70) |
Now plug in 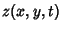 , set
, set  , and prime the indices to distinguish them from the
, and prime the indices to distinguish them from the 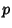 and
and 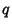 in (70),
in (70),
Making use of (64) in (71),
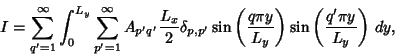 |
(72) |
so the sums over  and
and  collapse to a single term
collapse to a single term
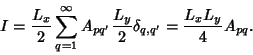 |
(73) |
Equating (72) and (73) and solving for 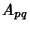 then gives
then gives
![\begin{displaymath}
A_{pq} = {4\over L_xL_y} \int_0^{L_y}\left[{\int_0^{L_x} z(x...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_294.gif) |
(74) |
An analogous derivation gives the 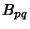 s as
s as
![\begin{displaymath}
B_{pq} = {4\over \omega_{pq}L_xL_y} \int_0^{L_y}\left[{\int_...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_295.gif) |
(75) |
The equation of motion for a membrane shaped as a Right Isosceles Triangle of length
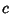 on a side and with the sides oriented along the Positive
on a side and with the sides oriented along the Positive 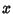 and
and  axes is given by
axes is given by
![$\psi(x,y,t)=[C_{pq}\cos(\omega_{pq} t)+D_{pq}\sin(\omega_{pq} t)]$](w_297.gif)
|
|
![$ \times \left[{\sin\left({p\pi x\over c}\right)\sin\left({q\pi y\over c}\right)-\sin\left({q\pi x\over c}\right)\sin\left({p\pi y\over c}\right)}\right],$](w_298.gif)
|
|
|
|
(76) |
where
 |
(77) |
and 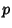 ,
, 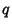 Integers with
Integers with 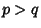 . This solution can be obtained by subtracting two wave solutions for a
square membrane with the indices reversed. Since points on the diagonal which are equidistant from the center must have the
same wave equation solution (by symmetry), this procedure gives a wavefunction which will vanish along the diagonal as
long as
. This solution can be obtained by subtracting two wave solutions for a
square membrane with the indices reversed. Since points on the diagonal which are equidistant from the center must have the
same wave equation solution (by symmetry), this procedure gives a wavefunction which will vanish along the diagonal as
long as 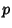 and
and 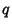 are both Even or Odd. We must further restrict the modes since those with
are both Even or Odd. We must further restrict the modes since those with  give
wavefunctions which are just the Negative of
give
wavefunctions which are just the Negative of 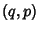 and
and 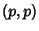 give an identically zero wavefunction. The following
plots show (3, 1), (4, 2), (5, 1), and (5,3).
give an identically zero wavefunction. The following
plots show (3, 1), (4, 2), (5, 1), and (5,3).
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Wave Equation in Prolate and Oblate Spheroidal Coordinates.'' §21.5 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 752-753, 1972.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 124-125, 1953.
© 1996-9 Eric W. Weisstein
1999-05-26
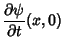
![]() devised his solution in 1746, and Euler
devised his solution in 1746, and Euler ![]() subsequently expanded the method in 1748. Let
subsequently expanded the method in 1748. Let
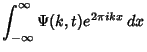
![$\displaystyle \int_{-\infty}^\infty [A(k)e^{2\pi ikvt}+B(k)e^{-2\pi ikvt}]e^{-2\pi ikx}\,dk$](w_169.gif)
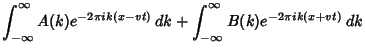
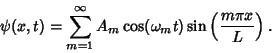
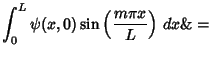
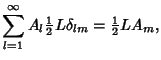
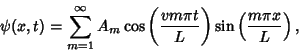
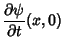
![\begin{displaymath}
\psi(x,t) = \sum_{n=1}^\infty \sin\left({n\pi x\over L}\right)e^{-v^2bt/2} [a_n\sin(\mu_nt)+b_n\cos(\mu_nt)],
\end{displaymath}](w_211.gif)

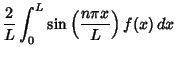
![$\displaystyle {2\over L\mu_n}\left\{{\int_0^L \sin\left({n\pi x\over L}\right)\left[{g(x)+ {v^2b\over 2} f(x)}\right]\,dx}\right\}.$](w_217.gif)
![]() and
and ![]() (in the absence of
gravity
(in the absence of
gravity ![]() ), use the 2-D wave equation
), use the 2-D wave equation

![]() and
and ![]() , so the final solution is
, so the final solution is
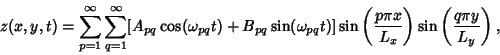

![]() and
and
![]() , we can compute the
, we can compute the ![]() s and
s and
![]() s explicitly. To accomplish this, we make use of the orthogonality of the Sine function in the form
s explicitly. To accomplish this, we make use of the orthogonality of the Sine function in the form
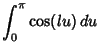
![\begin{displaymath}
I=\int_0^{L_y}\left[{\int_0^{L_x} z(x,y,0)\sin\left({p\pi x\...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_284.gif)
![$\displaystyle \sum_{q'=1}^\infty\int_0^{L_y}\left[{\sum_{p'=1}^\infty A_{p'q'}\...
...in\left({p\pi x\over L_x}\right)\sin\left({p'\pi x\over L_x}\right)\,dx}\right]$](w_287.gif)
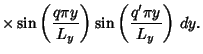
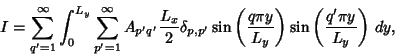
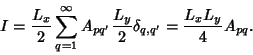
![\begin{displaymath}
A_{pq} = {4\over L_xL_y} \int_0^{L_y}\left[{\int_0^{L_x} z(x...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_294.gif)
![\begin{displaymath}
B_{pq} = {4\over \omega_{pq}L_xL_y} \int_0^{L_y}\left[{\int_...
...L_x}\right)\,dx}\right]\sin\left({q\pi y\over L_y}\right)\,dy.
\end{displaymath}](w_295.gif)
![]() on a side and with the sides oriented along the Positive
on a side and with the sides oriented along the Positive ![]() and
and ![]() axes is given by
axes is given by
