|
|
|
Applying the Stellation process to the Icosahedron gives
Of these, 32 have full icosahedral symmetry and 27 are Enantiomeric forms. Four are Polyhedron Compounds, one is a Kepler-Poinsot Solid, and one is the Dual Polyhedron of an Archimedean Solid. The only Stellations of Platonic Solids which are Uniform Polyhedra are the three Dodecahedron Stellations the Great Icosahedron (stellation # 11).
| name | |
| 1 | Icosahedron |
| 2 | Triakis Icosahedron |
| 3 | Octahedron 5-Compound |
| 4 | Echidnahedron |
| 11 | Great Icosahedron |
| 18 | Tetrahedron 10-Compound |
| 20 | Deltahedron-60 |
| 36 | Tetrahedron 5-Compound |




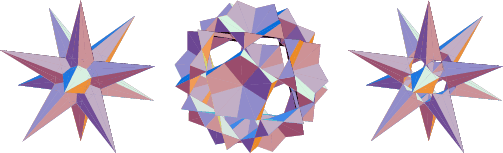

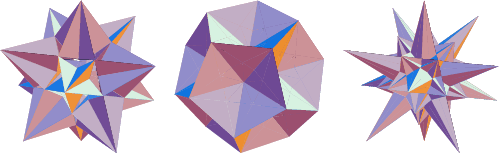













See also Archimedean Solid Stellation, Dodecahedron Stellations, Stellation
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 146-147, 1987.
Bulatov, V. ``Stellations of Icosahedron.'' http://www.physics.orst.edu/~bulatov/polyhedra/icosahedron/.
Coxeter, H. S. M. The Fifty-Nine Icosahedra. New York: Springer-Verlag, 1982.
Hart, G. W. ``59 Stellations of the Icosahedron.''
http://www.li.net/~george/virtual-polyhedra/stellations-icosahedron-index.html.
Maeder, R. E. Icosahedra.m notebook.
http://www.inf.ethz.ch/department/TI/rm/programs.html.
Maeder, R. E. ``The Stellated Icosahedra.'' Mathematica in Education 3, 1994.
ftp://ftp.inf.ethz.ch/doc/papers/ti/scs/icosahedra94.ps.gz.
Maeder, R. E. ``Stellated Icosahedra.''
http://www.mathconsult.ch/showroom/icosahedra/.
Wang, P. ``Polyhedra.''
http://www.ugcs.caltech.edu/~peterw/portfolio/polyhedra/.
Wenninger, M. J. Polyhedron Models. New York: Cambridge University Press, pp. 41-65, 1989.
Wheeler, A. H. ``Certain Forms of the Icosahedron and a Method for Deriving and Designating Higher Polyhedra.''
Proc. Internat. Math. Congress 1, 701-708, 1924.
|
|
|
© 1996-9 Eric W. Weisstein