Let B, A, and e be square matrices with e small, and define
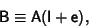 |
(1) |
where I is the Identity Matrix. Then the inverse of
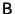 is approximately
is approximately
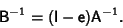 |
(2) |
This can be seen by multiplying
Note that if we instead let
 , and look for an inverse of the form
, and look for an inverse of the form
 , we obtain
, we obtain
In order to eliminate the
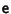 term, we require
term, we require
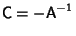 . However, then
. However, then
 , so
, so
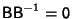 so there can be no inverse of this form.
so there can be no inverse of this form.
The exact inverse of
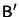 can be found as follows.
can be found as follows.
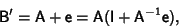 |
(5) |
so
![\begin{displaymath}
{\hbox{\sf B}}'^{-1}=[{\hbox{\sf A}}({\hbox{\sf I}}+{\hbox{\sf A}}^{-1}{\hbox{\sf e}})]^{-1}.
\end{displaymath}](i_486.gif) |
(6) |
Using a general Matrix Inverse identity then gives
 |
(7) |
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , and look for an inverse of the form
, and look for an inverse of the form
![]() , we obtain
, we obtain
![]() can be found as follows.
can be found as follows.