|
|
|
For Jacobi Elliptic Functions
![]() ,
,
![]() , and
, and
![]() ,
,
 |
|||
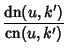 |
See also Jacobi Elliptic Functions
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 592 and 595, 1972.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, p. 505, 1990.