|
|
|
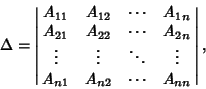
Let ![]() be an
be an ![]() -rowed Minor of the
-rowed Minor of the ![]() th order Determinant
th order Determinant
![]() associated with an
associated with an ![]() Matrix
Matrix
![]() in which the rows
in which the rows ![]() ,
, ![]() , ...,
, ..., ![]() are represented with columns
are represented with columns ![]() ,
, ![]() ,
...,
,
..., ![]() . Define the complementary minor to
. Define the complementary minor to ![]() as the
as the ![]() -rowed Minor obtained from
-rowed Minor obtained from
![]() by deleting all the rows and columns associated with
by deleting all the rows and columns associated with ![]() and the signed complementary minor
and the signed complementary minor ![]() to
to ![]() to be
to be
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1109-1100, 1979.