|
|
|
The second Knot Polynomial discovered. Unlike the first-discovered Alexander Polynomial, the Jones polynomial
can sometimes distinguish handedness (as can its more powerful generalization, the HOMFLY Polynomial). Jones
polynomials are Laurent Polynomials in ![]() assigned to an
assigned to an ![]() Knot. The Jones
polynomials are denoted
Knot. The Jones
polynomials are denoted ![]() for Links,
for Links, ![]() for Knots, and normalized so that
for Knots, and normalized so that
| (1) |
| (2) |
If a Link has an Odd number of components, then ![]() is a Laurent Polynomial over the
Integers; if the number of components is Even,
is a Laurent Polynomial over the
Integers; if the number of components is Even, ![]() is
is ![]() times a Laurent Polynomial.
The Jones polynomial of a Knot Sum
times a Laurent Polynomial.
The Jones polynomial of a Knot Sum ![]() satisfies
satisfies
| (3) |
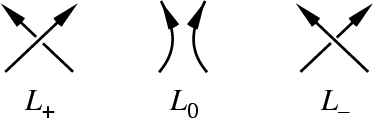
The Skein Relationship for under- and overcrossings is
| (4) |
Some interesting identities from Jones (1985) follow. For any Link ![]() ,
,
| (5) |
| (6) |
| (7) |
| (8) |
Let ![]() denote the Mirror Image of a Knot
denote the Mirror Image of a Knot ![]() . Then
. Then
| (9) |
| (10) | |||
| (11) |
Jones defined a simplified trace invariant for knots by
| (12) |
| (13) |
Jones polynomials were subsequently generalized to the two-variable HOMFLY Polynomials, the
relationship being
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Birman and Lin (1993) showed that substituting the Power Series for ![]() as the variable in the Jones
polynomial yields a Power Series whose Coefficients are Vassiliev
Polynomials.
as the variable in the Jones
polynomial yields a Power Series whose Coefficients are Vassiliev
Polynomials.
Let ![]() be an oriented connected Link projection of
be an oriented connected Link projection of ![]() crossings, then
crossings, then
| (19) |
There exist distinct Knots with the same Jones polynomial. Examples include (05-001, 10-132), (08-008, 10-129), (08-016, 10-156), (10-025, 10-056), (10-022, 10-035), (10-041, 10-094), (10-043, 10-091), (10-059, 10-106), (10-060, 10-083), (10-071, 10-104), (10-073, 10-086), (10-081, 10-109), and (10-137, 10-155) (Jones 1987). Incidentally, the first four of these also have the same HOMFLY Polynomial.
Witten (1989) gave a heuristic definition in terms of a topological quantum field theory, and Sawin (1996) showed that the
``quantum group'' ![]() gives rise to the Jones polynomial.
gives rise to the Jones polynomial.
See also Alexander Polynomial, HOMFLY Polynomial, Kauffman Polynomial F, Knot, Link, Vassiliev Polynomial
References
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York:
W. H. Freeman, 1994.
Birman, J. S. and Lin, X.-S. ``Knot Polynomials and Vassiliev's Invariants.'' Invent. Math. 111, 225-270, 1993.
Doll, H. and Hoste, J. ``A Tabulation of Oriented Links.'' Math. Comput. 57, 747-761, 1991.
Jones, V. ``A Polynomial Invariant for Knots via von Neumann Algebras.'' Bull. Am. Math. Soc. 12, 103-111, 1985.
Jones, V. ``Hecke Algebra Representations of Braid Groups and Link Polynomials.'' Ann. Math. 126, 335-388, 1987.
Lickorish, W. B. R. and Millett, B. R. ``The New Polynomial Invariants of Knots and Links.''
Math. Mag. 61, 1-23, 1988.
Murasugi, K. ``Jones Polynomials and Classical Conjectures in Knot Theory.'' Topology 26, 297-307, 1987.
Praslov, V. V. and Sossinsky, A. B.
Knots, Links, Braids and 3-Manifolds: An Introduction to the New Invariants in Low-Dimensional Topology.
Providence, RI: Amer. Math. Soc., 1996.
Sawin, S. ``Links, Quantum Groups, and TQFTS.'' Bull. Amer. Math. Soc. 33, 413-445, 1996.
Stoimenow, A. ``Jones Polynomials.'' http://www.informatik.hu-berlin.de/~stoimeno/ptab/j10.html.
Thistlethwaite, M. ``A Spanning Tree Expansion for the Jones Polynomial.'' Topology 26, 297-309, 1987.
Witten, E. ``Quantum Field Theory and the Jones Polynomial.'' Comm. Math. Phys. 121, 351-399, 1989.
![]() Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
Weisstein, E. W. ``Knots and Links.'' Mathematica notebook Knots.m.
|
|
|
© 1996-9 Eric W. Weisstein