An Unbiased Estimator of the Cumulants  of a Distribution. The expectation values of the
of a Distribution. The expectation values of the 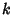 -statistics are therefore given by the corresponding
Cumulants
-statistics are therefore given by the corresponding
Cumulants
(Kenney and Keeping 1951, p. 189). For a sample of size, 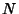 , the first few
, the first few 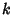 -statistics are given by
-statistics are given by
where 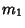 is the sample Mean,
is the sample Mean, 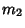 is the sample Variance, and
is the sample Variance, and 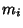 is the sample
is the sample 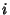 th Moment about the
Mean (Kenney and Keeping 1951, pp. 109-110, 163-165, and 189; Kenney and Keeping 1962). These statistics are obtained
from inverting the relationships
th Moment about the
Mean (Kenney and Keeping 1951, pp. 109-110, 163-165, and 189; Kenney and Keeping 1962). These statistics are obtained
from inverting the relationships
The first moment (sample Mean) is
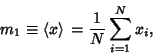 |
(14) |
and the expectation value is
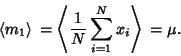 |
(15) |
The second Moment (sample Standard Deviation) is
and the expectation value is
since there are 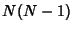 terms
terms 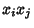 , using
, using
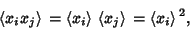 |
(18) |
and where 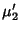 is the Moment about 0. Using the identity
is the Moment about 0. Using the identity
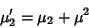 |
(19) |
to convert to the Moment 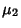 about the Mean and simplifying then gives
about the Mean and simplifying then gives
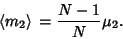 |
(20) |
The factor 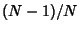 is known as Bessel's Correction.
is known as Bessel's Correction.
The third Moment is
Now use the identities
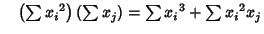
|
(22) |
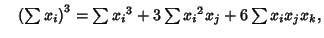
|
(23) |
where it is understood that sums over products of variables exclude equal indices. Plugging in
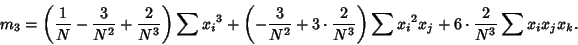 |
(24) |
The expectation value is then given by
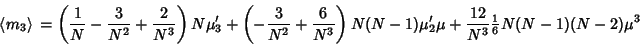 |
(25) |
where 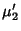 is the Moment about 0. Plugging in the identities
is the Moment about 0. Plugging in the identities
and simplifying then gives
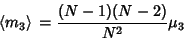 |
(28) |
(Kenney and Keeping 1951, p. 189).
The fourth Moment is
Now use the identities
Plugging in,
The expectation value is then given by
where 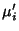 are Moments about 0. Using the identities
are Moments about 0. Using the identities
and simplifying gives
![\begin{displaymath}
\left\langle{m_4}\right\rangle{}={(N-1)[(N^2-3N+3)\mu_4+3(2N-3){\mu_2}^2]\over N^3}
\end{displaymath}](k_139.gif) |
(38) |
(Kenney and Keeping 1951, p. 189).
The square of the second moment is
Now use the identities
Plugging in,
The expectation value is then given by
where 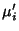 are Moments about 0. Using the identities
are Moments about 0. Using the identities
and simplifying gives
![\begin{displaymath}
\left\langle{{m_2}^2}\right\rangle{}={(N-1)[(N-1)\mu_4+(N^2-2N+3){\mu_2}^2]\over N^3}
\end{displaymath}](k_157.gif) |
(48) |
(Kenney and Keeping 1951, p. 189).
The Variance of 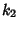 is given by
is given by
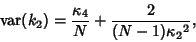 |
(49) |
so an unbiased estimator of
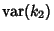 is given by
is given by
 |
(50) |
(Kenney and Keeping 1951, p. 189). The Variance of 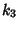 can be expressed in terms of Cumulants by
can be expressed in terms of Cumulants by
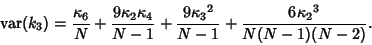 |
(51) |
An Unbiased Estimator for
 is
is
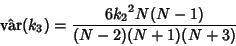 |
(52) |
(Kenney and Keeping 1951, p. 190).
Now consider a finite population. Let a sample of 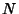 be taken from a population of
be taken from a population of 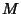 . Then Unbiased
Estimators
. Then Unbiased
Estimators 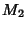 for the population Mean
for the population Mean  ,
, 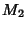 for the population Variance
for the population Variance 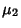 ,
,
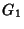 for the population Skewness
for the population Skewness  , and
, and 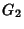 for the population Kurtosis
for the population Kurtosis 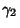 are
are
(Church 1926, p. 357; Carver 1930; Irwin and Kendall 1944; Kenney and Keeping 1951, p. 143), where  is the sample
Skewness and
is the sample
Skewness and 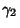 is the sample Kurtosis.
is the sample Kurtosis.
See also Gaussian Distribution, Kurtosis, Mean, Moment, Skewness, Variance
References
Carver, H. C. (Ed.). ``Fundamentals of the Theory of Sampling.'' Ann. Math. Stat. 1, 101-121, 1930.
Church, A. E. R. ``On the Means and Squared Standard-Deviations of Small Samples from Any Population.'' Biometrika 18,
321-394, 1926.
Irwin, J. O. and Kendall, M. G. ``Sampling Moments of Moments for a Finite Population.'' Ann. Eugenics 12, 138-142, 1944.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Kenney, J. F. and Keeping, E. S. ``The 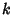 -Statistics.'' §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 99-100, 1962.
-Statistics.'' §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 99-100, 1962.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of a Distribution. The expectation values of the
of a Distribution. The expectation values of the ![]() -statistics are therefore given by the corresponding
Cumulants
-statistics are therefore given by the corresponding
Cumulants
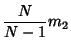

![$\displaystyle {N^2[(N+1)m_4-3(N-1){m_2}^2]\over(N-1)(N-2)(N-3)},$](k_67.gif)
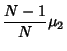
![$\displaystyle {(N-1)[(N-1)\mu_4+(N^2-2N+3){\mu_2}^2]\over N^3}$](k_77.gif)
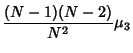
![$\displaystyle {(N-1)[(N^2-3N+3)\mu_4+3(2N-3){\mu_2}^2]\over N^3}.$](k_81.gif)
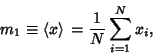
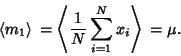

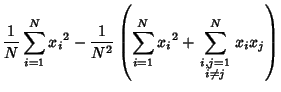

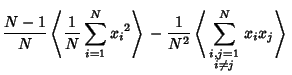

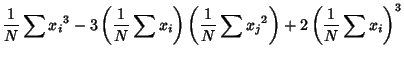
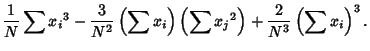
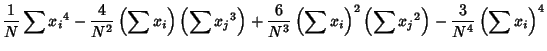
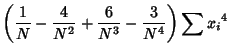
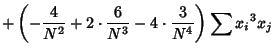
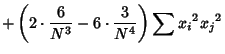
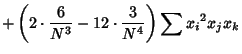
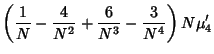
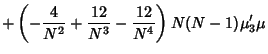

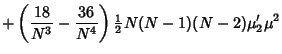
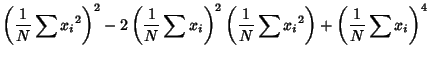
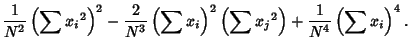
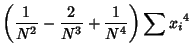
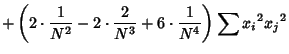
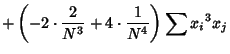
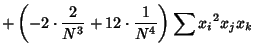
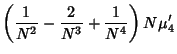
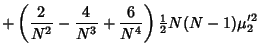
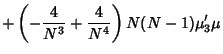
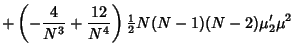
![]() is given by
is given by
![]() be taken from a population of
be taken from a population of ![]() . Then Unbiased
Estimators
. Then Unbiased
Estimators ![]() for the population Mean
for the population Mean ![]() ,
, ![]() for the population Variance
for the population Variance ![]() ,
,
![]() for the population Skewness
for the population Skewness ![]() , and
, and ![]() for the population Kurtosis
for the population Kurtosis ![]() are
are
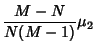
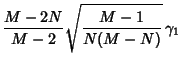
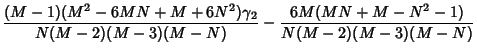
![]() -Statistics.'' §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 99-100, 1962.
-Statistics.'' §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed.
Princeton, NJ: Van Nostrand, pp. 99-100, 1962.