Knights Problem

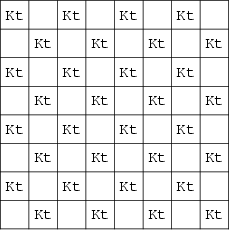
$\begin{figure}\begin{center}\BoxedEPSF{KnightsMax.epsf}\end{center}\end{figure}$

The problem of determining how many nonattacking knights can be placed on an $n\times n$ Chessboard. For , the solution is 32 (illustrated above). In general, the solutions are

$\begin{displaymath} K(n)=\cases{ {\textstyle{1\over 2}}n^2 & $n>2$\ even\cr {\textstyle{1\over 2}}(n^2+1) & $n>1$\ odd,\cr} \end{displaymath}$

giving the sequence 1, 4, 5, 8, 13, 18, 25, ... (Sloane's A030978, Dudeney 1970, p. 96; Madachy 1979).

$\begin{figure}\begin{center}\BoxedEPSF{KnightsMin.epsf}\end{center}\end{figure}$

The minimal number of knights needed to occupy or attack every square on an $n\times n$ Chessboard is given by 1, 4, 4, 4, 5, 8, 10, ... (Sloane's A006075). The number of such solutions are given by 1, 1, 2, 3, 8, 22, 3, ... (Sloane's A006076).

References

Dudeney, H. E. ``The Knight-Guards.'' §319 in Amusements in Mathematics. New York: Dover, p. 95, 1970.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 38-39, 1979.

Moser, L. ``King Paths on a Chessboard.'' Math. Gaz. 39, 54, 1955.

Sloane, N. J. A. Sequences A030978, A006076/M0884 and A006075/M3224 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 196-197, 1991.

Wilf, H. S. ``The Problem of Kings.'' Electronic J. Combinatorics 2, 3 1-7, 1995. http://www.combinatorics.org/Volume_2/volume2.html#3.