Lemon

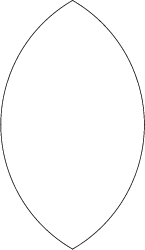
A Surface of Revolution defined by Kepler. It consists of less than half of a circular Arc rotated about an axis passing through the endpoints of the Arc. The equations of the upper and lower boundaries in the $xz$ plane are

$$z_\pm = \pm\sqrt{R^2-(x+r)^2}$$

for $R>r$ and $x\in [-(R-r), R-r]$. The Cross-Section of a lemon is a Lens. The lemon is the inside surface of a Spindle Torus.

See also Apple, Lens, Spindle Torus