|
|
|
|
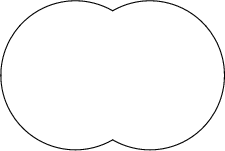
A Surface of Revolution defined by Kepler. ![]() It consists of more than half of a circular Arc
rotated about an axis passing through the endpoints of the Arc. The equations of the upper and lower boundaries in
the
It consists of more than half of a circular Arc
rotated about an axis passing through the endpoints of the Arc. The equations of the upper and lower boundaries in
the ![]() -
-![]() Plane are
Plane are
See also Bubble, Lemon, Sphere-Sphere Intersection, Spindle Torus