Magic Tour

Let a chess piece make a Tour on an $n\times n$ Chessboard whose squares are numbered from 1 to along the path of the chess piece. Then the Tour is called a magic tour if the resulting arrangement of numbers is a Magic Square. If the first and last squares traversed are connected by a move, the tour is said to be closed (or ``re-entrant''); otherwise it is open. The Magic Constant for the $8\times 8$ Chessboard is 260.

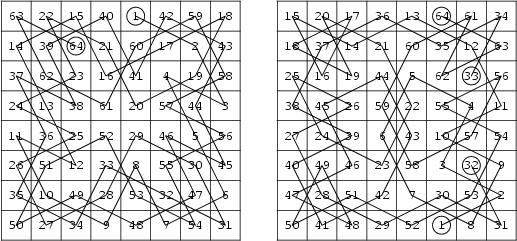
$\begin{figure}\begin{center}\BoxedEPSF{MagicToursAlmostKnights.epsf scaled 830}\end{center}\end{figure}$

Magic Knight's Tours are not possible on $n\times n$ boards for Odd, and are believed to be impossible for . The ``most magic'' knight tour known on the $8\times 8$ board is the Semimagic Square illustrated in the above left figure (Ball and Coxeter 1987, p. 185) having main diagonal sums of 348 and 168. Combining two half-knights' tours one above the other as in the above right figure does, however, give a Magic Square (Ball and Coxeter 1987, p. 185).

$\begin{figure}\begin{center}\BoxedEPSF{MagicTour.epsf scaled 1000}\end{center}\end{figure}$

The above illustration shows a $16\times 16$ closed magic Knight's Tour (Madachy 1979).

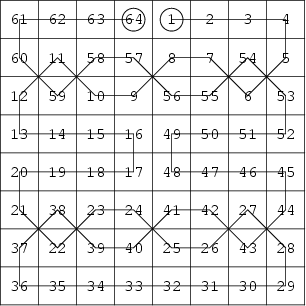
$\begin{figure}\begin{center}\BoxedEPSF{MagicTourKing.epsf}\end{center}\end{figure}$

A magic tour for king moves is illustrated above (Coxeter 1987, p. 186).

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 185-187, 1987.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 87-89, 1979.