|
|
|
Also called the Ménage Problem. In how many ways can ![]() married couples be seated around a
circular table in such a manner than there is always one man between two women and none of the men is next to his own wife?
The solution (Ball and Coxeter 1987, p. 50) uses Discordant Permutations and can be
given in terms of Laisant's Recurrence Formula
married couples be seated around a
circular table in such a manner than there is always one man between two women and none of the men is next to his own wife?
The solution (Ball and Coxeter 1987, p. 50) uses Discordant Permutations and can be
given in terms of Laisant's Recurrence Formula
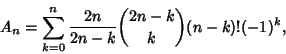
The first few values of ![]() are
are ![]() , 1, 0, 2, 13, 80, 579, ... (Sloane's A000179), which are sometimes called
Ménage Numbers. The desired solution is then
, 1, 0, 2, 13, 80, 579, ... (Sloane's A000179), which are sometimes called
Ménage Numbers. The desired solution is then ![]() . The numbers
. The numbers ![]() can be considered a
special case of a restricted Rooks Problem.
can be considered a
special case of a restricted Rooks Problem.
See also Discordant Permutation, Laisant's Recurrence Formula, Rooks Problem
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 50, 1987.
Dörrie, H. §8 in 100 Great Problems of Elementary Mathematics: Their History and Solutions.
New York: Dover, pp. 27-33, 1965.
Halmos, P. R.; Vaughan, H. E. ``The Marriage Problem.'' Amer. J. Math. 72, 214-215, 1950.
Lucas, E. Théorie des Nombres. Paris: A. Blanchard, pp. 215 and 491-495, 1979.
MacMahon, P. A. Combinatory Analysis, Vol. 1. London: Cambridge University Press, pp. 253-256, 1915.
Newman, D. J. ``A Problem in Graph Theory.'' Amer. Math. Monthly 65, 611, 1958.
Sloane, N. J. A. Sequence
A000179/M2062
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Touchard, J. ``Sur un problème de permutations.'' C. R. Acad. Sci. Paris 198, 631-633, 1934.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 123, 1991.
|
|
|
© 1996-9 Eric W. Weisstein