If
is the same for all paths in the Complex Plane, then 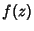 is said to be monogenic at
is said to be monogenic at 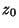 . Monogenic therefore
essentially means having a single Derivative at a point. Functions are either monogenic or have infinitely many
Derivatives (in which case they are called
Polygenic); intermediate cases are not possible.
. Monogenic therefore
essentially means having a single Derivative at a point. Functions are either monogenic or have infinitely many
Derivatives (in which case they are called
Polygenic); intermediate cases are not possible.
See also Polygenic Function
References
Newman, J. R. The World of Mathematics, Vol. 3. New York: Simon & Schuster, p. 2003, 1956.
© 1996-9 Eric W. Weisstein
1999-05-26