Perfect Square Dissection

A Square which can be Dissected into a number of smaller Squares with no two equal is called a Perfect Square Dissection (or a Squared Square). Square dissections in which the squares need not be different sizes are called Mrs. Perkins' Quilts. If no subset of the Squares forms a Rectangle, then the perfect square is called ``simple.'' Lusin claimed that perfect squares were impossible to construct, but this assertion was proved erroneous when a 55-Square perfect square was published by R. Sprague in 1939 (Wells 1991).

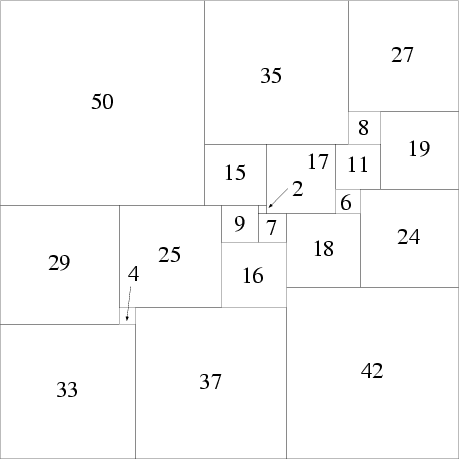
There is a unique simple perfect square of order 21 (the lowest possible order), discovered in 1978 by A. J. W. Duijvestijn (Bouwkamp and Duijvestijn 1992). It is composed of 21 squares with total side length 112, and is illustrated above. There is a simple notation (sometimes called Bouwkamp code) used to describe perfect squares. In this notation, brackets are used to group adjacent squares with flush tops, and then the groups are sequentially placed in the highest (and leftmost) possible slots. For example, the 21-square illustrated above is denoted [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].

The number of simple perfect squares of order $n$ for $n\geq 21$ are 1, 8, 12, 26, 160, 441, ... (Sloane's A006983). Duijvestijn's Table I gives a list of the 441 simple perfect squares of order 26, the smallest with side length 212 and the largest with side length 825. Skinner (1993) gives the smallest possible side length (and smallest order for each) as 110 (22), 112 (21), 120 (24), 139 (22), 140 (23), ... for simple perfect squared squares, and 175 (24), 235 (25), 288 (26), 324 (27), 325 (27), ... for compound perfect squared squares.

There are actually three simple perfect squares having side length 110. They are [60, 50], [23, 27], [24, 22, 14], [7, 16], [8, 6], [12, 15], [13], [2, 28], [26], [4, 21, 3], [18], [17] (order 22; discovered by A. J. W. Duijvestijn); [60, 50], [27, 23], [24, 22, 14], [4, 19], [8, 6], [3, 12, 16], [9], [2, 28], [26], [21], [1, 18], [17] (order 22; discovered by T. H. Willcocks); and [44, 29, 37], [21, 8], [13, 32], [28, 16], [15, 19], [12,4], [3, 1], [2, 14], [5], [10, 41], [38, 7], [31] (order 23; discovered by A. J. W. Duijvestijn).

D. Sleator has developed an efficient Algorithm for finding non-simple perfect squares using what he calls rectangle and ``ell'' grow sequences. This algorithm finds a slew of compound perfect squares of orders 24-32. Weisstein gives a partial list of known simple and compound perfect squares (where the number of simple perfect squares is exact for orders less than 27) as well as Mathematica ${}^{\scriptstyle\circledRsymbol}$ (Wolfram Research, Champaign, IL) algorithms for drawing them.

Order	# Simple	# Compound
21	1	0
22	8	0
23	12	0
24	26	1
25	160	1
26	441	2
27	?	2
28	?	4
29	?	2
30	?	3
31	?	2
32	?	2
38	1	0
69	1	0

See also Mrs. Perkins' Quilt

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 115-116, 1987.

Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, pp. 157-161, 1966.

Bouwkamp, C. J. and Duijvestijn, A. J. W. ``Catalogue of Simple Perfect Squared Squares of Orders 21 Through 25.'' Eindhoven Univ. Technology, Dept. Math, Report 92-WSK-03, Nov. 1992.

Brooks, R. L.; Smith, C. A. B.; Stone, A. H.; and Tutte, W. T. ``The Dissection of Rectangles into Squares.'' Duke Math. J. 7, 312-340, 1940.

Duijvestijn, A. J. W. ``A Simple Perfect Square of Lowest Order.'' J. Combin. Th. Ser. B 25, 240-243, 1978.

Duijvestijn, A. J. W. ``A Lowest Order Simple Perfect $2\times 1$ Squared Rectangle.'' J. Combin. Th. Ser. B 26, 372-374, 1979.

Duijvestijn, A. J. W. ftp://ftp.cs.utwente.nl/pub/doc/dvs/TableI.

Gardner, M. ``Squaring the Square.'' Ch. 17 in The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection. New York: Simon and Schuster, 1961.

Gardner, M. Fractal Music, Hypercards, and More: Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 172-174, 1992.

Kraitchik, M. Mathematical Recreations. New York: W. W. Norton, p. 198, 1942.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 15 and 32-33, 1979.

Mauldin, R. D. (Ed.) The Scottish Book: Math at the Scottish Cafe Boston, MA: Birkhäuser, 1982.

Moron, Z. ``O rozkadach prostokatów na kwadraty.'' Przeglad matematyczno-fizyczny 3, 152-153, 1925.

Skinner, J. D. II. Squared Squares: Who's Who & What's What. Published by the author, 1993.

Sloane, N. J. A. Sequence A006983/M4482 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Sprague, R. ``Beispiel einer Zerlegung des Quadrats in lauter verschiedene Quadrate.'' Math. Z. 45, 607-608, 1939.

Weisstein, E. W. ``Perfect Squares.'' Mathematica notebook PerfectSquare.m.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 242, 1991.