|
|
|
If all elements ![]() of an Irreducible Matrix
of an Irreducible Matrix
![]() are Nonnegative, then
are Nonnegative, then
![]() is an
Eigenvalue of
is an
Eigenvalue of
![]() and all the Eigenvalues of
and all the Eigenvalues of
![]() lie on the Disk
lie on the Disk
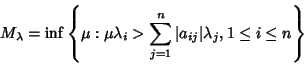
See also Wielandt's Theorem
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1121, 1979.