|
|
|
For
![]() , define
, define
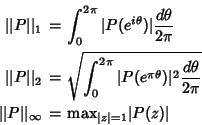
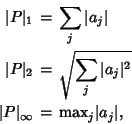
See also Bombieri Norm, Norm, Unit Circle
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, p. 151, 1989.