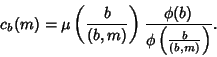The sum
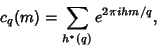 |
(1) |
where 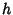 runs through the residues Relatively Prime to
runs through the residues Relatively Prime to 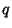 , which is important in the representation of numbers by the
sums of squares. If
, which is important in the representation of numbers by the
sums of squares. If 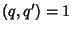 (i.e.,
(i.e., 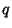 and
and 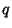 ' are Relatively Prime), then
' are Relatively Prime), then
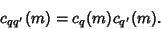 |
(2) |
For argument 1,
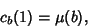 |
(3) |
where 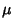 is the Möbius Function, and for general
is the Möbius Function, and for general 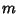 ,
,
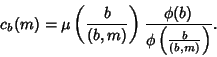 |
(4) |
See also Möbius Function, Weyl's Criterion
References
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, p. 254, 1991.
© 1996-9 Eric W. Weisstein
1999-05-25