|
|
|
The constant ![]() in the Laurent Series
in the Laurent Series
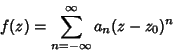
See also Contour Integration, Laurent Series, Residue Theorem
References
Arfken, G. ``Calculus of Residues.'' §7.2 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 400-421, 1985.