|
|
|
|
The Dual Polyhedron of the Cuboctahedron, also sometimes called the Rhomboidal Dodecahedron (Cotton
1990). Its 14 vertices are joined by 12 Rhombuses, and one possible way to construct it is known as the
Bauspiel. The rhombic dodecahedron is a Zonohedron and a Space-Filling Polyhedron. The vertices are
given by (![]() ,
, ![]() ,
, ![]() ), (
), (![]() , 0, 0), (0,
, 0, 0), (0, ![]() , 0), (0, 0,
, 0), (0, 0, ![]() ).
).
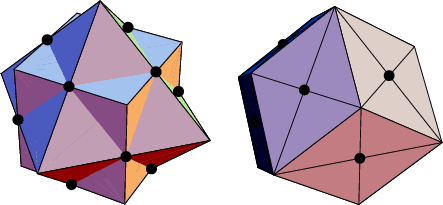
The edges of the Cube-Octahedron Compound intersecting in the points plotted above are the diagonals of Rhombuses, and the 12 Rhombuses form a rhombic dodecahedron (Ball and Coxeter 1987).
See also Bauspiel, Cube-Octahedron Compound, Dodecahedron, Pyritohedron, Rhombic Triacontahedron, Rhombus, Trigonal Dodecahedron, Zonohedron
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 137, 1987.
Cotton, F. A. Chemical Applications of Group Theory, 3rd ed. New York: Wiley, p. 62, 1990.