|
|
|
|
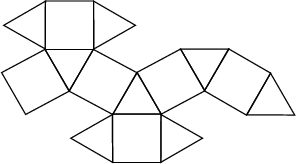
An Archimedean Solid (also called the Dymaxion or Heptaparallelohedron) whose Dual is the Rhombic Dodecahedron. It is one of the two convex Quasiregular Polyhedra and has Schläfli Symbol
![]() . It is also Uniform
Polyhedron
. It is also Uniform
Polyhedron ![]() and has Wythoff Symbol
and has Wythoff Symbol ![]() . Its faces are
. Its faces are ![]() . It has the
. It has the ![]() Octahedral Group of symmetries.
Octahedral Group of symmetries.
The Vertices of a cuboctahedron with Edge length of ![]() are
are
![]() ,
,
![]() , and
, and
![]() . The Inradius, Midradius, and
Circumradius for
. The Inradius, Midradius, and
Circumradius for ![]() are
are
|
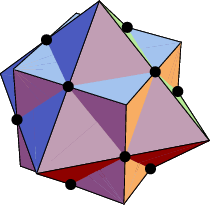
The solid common to both the Cube and Octahedron (left figure) in a Cube-Octahedron Compound is a Cuboctahedron (right figure; Ball and Coxeter 1987).
See also Archimedean Solid, Cube, Cube-Octahedron Compound, Cubohemioctahedron, Octahedron, Octahemioctahedron, Quasiregular Polyhedron, Rhombic Dodecahedron, Rhombus
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, p. 137, 1987.
Ghyka, M. The Geometry of Art and Life. New York: Dover, p. 54, 1977.
|
|
|
© 1996-9 Eric W. Weisstein